Question

Can someone explain how to do the algebra for this question? I know everything else, I just don’t know how to rearrange the question to solve for v.

Answer 1

Refer to the step-by-step Explanation.

Explanation:

Simplify the equation with given substitutions,

Given Equation:

`mgh+(1/2)mv^2+(1/2)I \omega^2=(1/2)mv_{_(0)}^2+(1/2)I \omega_{_(0)}^2`

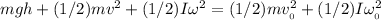
Given Substitutions:

`\omega=v/R\\\\ \omega_{_(0)}=v_{_(0)}/R\\\\\ I=(2/5)mR^2`
`\hrulefill`

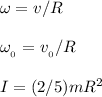
Start by substituting in the appropriate values:
`mgh+(1/2)mv^2+(1/2)I \omega^2=(1/2)mv_{_(0)}^2+(1/2)I \omega_{_(0)}^2 \\\\\\\\\Longrightarrow mgh+(1/2)mv^2+(1/2)\bold{[(2/5)mR^2]} \bold{[v/R]}^2=(1/2)mv_{_(0)}^2+(1/2)\bold{[(2/5)mR^2]}\bold{[v_{_(0)}/R]}^2`

Adjusting the equation so it easier to work with.
`\Longrightarrow mgh+(1)/(2) mv^2+(1)/(2) \Big[(2)/(5) mR^2\Big]\Big[(v)/(R) \Big]^2=\frac12mv_{_(0)}^2+\frac12\Big[\frac25mR^2\Big]\Big[\frac{v_{_(0)}}{R}\Big]^2`

`\hrulefill`

Simplifying the left-hand side of the equation:

`mgh+(1)/(2) mv^2+(1)/(2) \Big[(2)/(5) mR^2\Big]\Big[(v)/(R) \Big]^2`

Simplifying the third term.

`\Longrightarrow mgh+(1)/(2) mv^2+(1)/(2) \Big[(2)/(5) mR^2\Big]\Big[(v)/(R) \Big]^2\\\\\\\\\Longrightarrow mgh+(1)/(2) mv^2+(1)/(2)\cdot (2)/(5) \Big[mR^2\Big]\Big[(v)/(R) \Big]^2\\\\\\\\\Longrightarrow mgh+(1)/(2) mv^2+(1)/(5) \Big[mR^2\Big]\Big[(v)/(R) \Big]^2`

`\\ \boxed{\left\begin{array}{ccc}\text{\Underline{Power of a Fraction Rule:}}\\\\\Big((a)/(b)\Big)^2=(a^2)/(b^2) \end{array}\right }`

`\Longrightarrow mgh+(1)/(2) mv^2+(1)/(5) \Big[mR^2\Big]\Big[(v^2)/(R^2) \Big]\\\\\\\\\Longrightarrow mgh+(1)/(2) mv^2+(1)/(5) \Big[mR^2 \cdot(v^2)/(R^2) \Big]`

"R²'s" cancel, we are left with:

`\Longrightarrow mgh+(1)/(2) mv^2+(1)/(5) \Big[mR^2\Big]\Big[(v^2)/(R^2) \Big]\\\\\\\\\Longrightarrow mgh+(1)/(2) mv^2+(1)/(5)mv^2`

We have like terms, combine them.

`\Longrightarrow mgh+(1)/(2) mv^2+(1)/(5) \Big[mR^2\Big]\Big[(v^2)/(R^2) \Big]\\\\\\\\\Longrightarrow mgh+(7)/(10) mv^2`

Each term has an "m" in common, factor it out.

`\Longrightarrow m(gh+(7)/(10)v^2)`

Now we have the following equation:

`\Longrightarrow m(gh+(7)/(10)v^2)=\frac12mv_{_(0)}^2+\frac12\Big[\frac25mR^2\Big]\Big[\frac{v_{_(0)}}{R}\Big]^2`

`\hrulefill`

Simplifying the right-hand side of the equation:

`\Longrightarrow \frac12mv_{_(0)}^2+\frac12\cdot\frac25\Big[mR^2\Big]\Big[\frac{v_{_(0)}}{R}\Big]^2\\\\\\\\\Longrightarrow \frac12mv_{_(0)}^2+\frac15\Big[mR^2\Big]\Big[\frac{v_{_(0)}}{R}\Big]^2\\\\\\\\\Longrightarrow \frac12mv_{_(0)}^2+\frac15\Big[mR^2\Big]\Big[\frac{v_{_(0)}^2}{R^2}\Big]\\\\\\\\\Longrightarrow \frac12mv_{_(0)}^2+\frac15\Big[mR^2\cdot\frac{v_{_(0)}^2}{R^2}\Big]\\\\\\\\\Longrightarrow \frac12mv_{_(0)}^2+\frac15mv_{_(0)}^2\Big\\\\\\\\`

`\Longrightarrow (7)/(10)mv_{_(0)}^2`

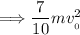
Now we have the equation:

`\Longrightarrow m(gh+(7)/(10)v^2)=(7)/(10)mv_{_(0)}^2`

`\hrulefill`

Now solving the equation for the variable "v":

`m(gh+(7)/(10)v^2)=(7)/(10)mv_{_(0)}^2`

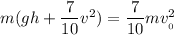
Dividing each side by "m," this will cancel the "m" variable on each side.

`\Longrightarrow gh+(7)/(10)v^2=(7)/(10)v_{_(0)}^2`

Subtract the term "gh" from either side of the equation.

`\Longrightarrow (7)/(10)v^2=(7)/(10)v_{_(0)}^2-gh`

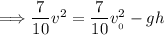
Multiply each side of the equation by "10/7."

`\Longrightarrow v^2=(10)/(7)\cdot(7)/(10)v_{_(0)}^2-(10)/(7)gh\\\\\\\\\Longrightarrow v^2=v_{_(0)}^2-(10)/(7)gh`

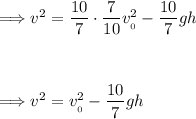
Now squaring both sides.

`\Longrightarrow \boxed{\boxed{v=\sqrt{v_{_(0)}^2-(10)/(7)gh}}}`

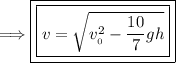
Thus, the simplified equation above matches the simplified equation that was given.