Question

HELP ME PLEASEEEEEEEE!!!

Answer 1

Refer to the explanation.

Step-by-step explanation:

Newton's Law of Universal Gravitation states that every particle or object in the universe attracts every other particle or object with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Mathematically, it is expressed as:

`F_g=(Gm_1m_2)/(d^2)`

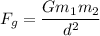
Where...

• "F_g" represents the magnitude of the gravitational force between two objects.

• "G" is the gravitational constant (which is approximately 6.67430 × 10⁻¹¹ N m²/kg²).

• "m₁" and "m₂" are the masses of the two objects.
• "d" is the distance between the centers of the two objects.

This law describes the gravitational interaction between any two objects in the universe, whether they are planets, stars, or even smaller particles. It helps explain the motion of celestial bodies, the orbits of planets around the sun, and many other gravitational phenomena observed in the universe.

`\hrulefill`

We are given a set of questions revolved around Newton's Law of Universal Gravitation that we are asked to answer. So please follow along carefully.

Question (1) - What happens to "F_g" if "m₁" is increased by a factor of 5x?

If mass #1 is increased by a factor of 5x, the magnitude of the force would also increase by a factor of 5x. According to Newton's Law of Universal Gravitation, the force is directly proportional to the mass of object #1.

We can prove this mathematically,

`\text{We have,} \ F_g=(Gm_1m_2)/(d^2). \ \text{Denoting the new force as} \ F_n; \ m_1 \rightarrow 5m_1\\\\\\\Longrightarrow F_n=(G(5)m_1m_2)/(d^2)\\\\\\\\\Longrightarrow F_n=5(Gm_1m_2)/(d^2)\\\\\\\\\Longrightarrow \boxed{F_n=5(F_g)}`

Question (2) - What happens to "F_g" if "m₂" is increased by a factor of 7x?

If mass #2 is increased by a factor of 7x, the magnitude of the force would also increase by a factor of 7x. Similarly, the force is directly proportional to the mass of object #2.

Proving this mathematically,

`\text{We have,} \ F_g=(Gm_1m_2)/(d^2); \ m_2 \rightarrow 7m_2\\\\\\\Longrightarrow F_n=(Gm_1(7)m_2)/(d^2)\\\\\\\\\Longrightarrow F_n=7(Gm_1m_2)/(d^2)\\\\\\\\\Longrightarrow \boxed{F_n=7(F_g)}`

Question (3) - What happens to "F_g" if "m₁" and "m₂" are increased by a factor of 5x?

If both masses are increased by a factor of 5x, the magnitude of the force would increase by a factor of 25x (5x multiplied by 5x). The force is directly proportional to the product of the masses, so increasing both masses by the same factor results in an increase in the force by the square of that factor.

Proving this mathematically,

`\text{We have,} \ F_g=(Gm_1m_2)/(d^2); \ m_1 \rightarrow 5m_1 \ and \ m_2 \rightarrow 5m_2\\\\\\\Longrightarrow F_n=(G(5)m_1(5)m_2)/(d^2)\\\\\\\\\Longrightarrow F_n=(5)(5)(Gm_1m_2)/(d^2)\\\\\\\\\Longrightarrow \boxed{F_n=25(F_g)}`

Question (4) - What happens to "F_g" if "d" is increased by a factor of 9x?

If the distance between the two masses is increased by a factor of 9x, the magnitude of the force would decrease by a factor of 1/81 (1/9x multiplied by 1/9x). The force is inversely proportional to the square of the distance between the masses.

Proving this mathematically,

`\text{We have,} \ F_g=(Gm_1m_2)/(d^2); \ d \rightarrow 9d\\\\\\\Longrightarrow F_n=(Gm_1m_2)/((9d)^2)\\\\\\\\\Longrightarrow F_n=(1)/(81) \cdot (Gm_1m_2)/(d^2)\\\\\\\\\Longrightarrow \boxed{F_n=(1)/(81)(F_g)}`

Question (5) - What happens to "F_g" if "d" is decreased by a factor of 9x?

If the distance between the two masses is decreased by a factor of 9x, the magnitude of the force would increase by a factor of 81 (9x multiplied by 9x). Again, the force is inversely proportional to the square of the distance, so decreasing the distance leads to a significant increase in the force.

Proving this mathematically,

`\text{We have,} \ F_g=(Gm_1m_2)/(d^2); \ d \rightarrow (1)/(9)d\\\\\\\Longrightarrow F_n=(Gm_1m_2)/(\Big((1)/(9)d\Big)^2)\\\\\\\\\Longrightarrow F_n=81 (Gm_1m_2)/(d^2)\\\\\\\\\Longrightarrow \boxed{F_n=81(F_g)}`

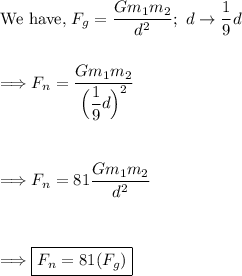
Question (6) - What happens to "F_g" if all variables are increased by a factor of 7x?

If all variables (masses and distance) are increased by a factor of 7x, the magnitude of the force would remain unchanged.

Once again proving this mathematically,

`\text{We have,} \ F_g=(Gm_1m_2)/(d^2); \ m_1, \ m_2, \ d \rightarrow 7m_1, \ 7m_2, \ 7d\\\\\\\Longrightarrow F_n=(G(7)m_1(7)m_2)/((7d)^2)\\\\\\\\\Longrightarrow F_n=((7)(7))/(49) \cdot (Gm_1m_2)/(d^2)\\\\\\\\\Longrightarrow \boxed{F_n=F_g}`

Question (7) - Fill in the blanks of the given paragraph.

Newton's Law of Universal gravitation tells us that the gravitational force is directly proportional to the masses and inversely proportional to the square of the distance between the masses.