Question

find the limit. use l'hospital's rule where appropriate. if there is a more elementary method, consider using it. lim x→0 6x − sin(6x) 6x − tan(6x)

Answer 1

-1/2

Explanation:

You want the limit as x→0 of the ratio (6x -sin(6x))/(6x -tan(6x)).

L'Hôpital's rule

The given expression evaluates at x=0 to (0 -0)/(0 -0) = 0/0, an indeterminate form. Hence, L'Hôpital's rule applies.

The ratio of derivatives of the numerator and denominator is ...

(6 -6cos(6x))/(6 -6sec²(6x))

which still evaluates to 0/0 at x=0.

Applying L'Hôpital's rule a second time gives ...

`(36\sin(6x))/(-72\sec^2(6x)\tan(6x))=(-\cos^3(6x))/(2)`

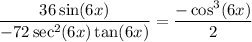
At x=0, this evaluates to -1/2.

The limit as x→0 is -1/2.

__

Additional comment

We like to check these limits using a graphing calculator. The graph is in the second attachment.

<95141404393>