Question

Consider CD. Describe the set of all points in space that are equidistant from C and D .

Answer 1

The set of all points in space that are equidistant from points C and D forms the perpendicular bisector of the line segment CD.

Step-by-step explanation:

Consider points C and D in space. The set of all points equidistant from C and D is the perpendicular bisector of the line segment CD. This can be explained by the definition of the perpendicular bisector, which states that any point on the perpendicular bisector is equidistant from the endpoints of the line segment. Let M be the midpoint of CD. The line passing through M and perpendicular to CD is the perpendicular bisector. Any point P on this line satisfies the condition PC = PD, making it equidistant from C and D.

To understand this geometrically, envision CD as a line segment. The midpoint M is the point equidistant from C and D. Now, any point on the perpendicular bisector through M is equidistant from C and D. This is due to the fact that the perpendicular bisector forms right angles with the line segment CD. Using the Pythagorean Theorem, the distances from any point on the perpendicular bisector to C and D are equal, confirming their equidistance.

In mathematical terms, le
`t \( \overrightarrow{CD} = \overrightarrow{D} - \overrightarrow{C} \),` and the midpoint M is given by
`\( \overrightarrow{M} = (1)/(2) (\overrightarrow{C} + \overrightarrow{D}) \).`The vector equation of the perpendicular bisector is
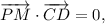`\( \overrightarrow{PM} \cdot \overrightarrow{CD} = 0 \),` where P is any point on the bisector. This equation expresses the perpendicularity, ensuring that any point P on the bisector is equidistant from C and D.