Question

PLS HELP!!!!

Question 2
The vertex form of the equation of a horizontal parabola is given by
, where (h, k) is the vertex of the parabola and the absolute value of p is the distance from the vertex to the focus, which is also the distance from the vertex to the directrix. You will use GeoGebra to create a horizontal parabola and write the vertex form of its equation. Open GeoGebra, and complete each step below.

Part A
Mark the focus of the parabola you are going to create at F(-5, 2). Draw a vertical line that is 8 units to the right of the focus. This line will be the directrix of your parabola. What is the equation of the line?
















Part B
Construct the line that is perpendicular to the directrix and passes through the focus. This line will be the axis of symmetry of the parabola. What are the coordinates of the point of intersection, A, of the axis of symmetry and the directrix of the parabola?















Part C
Explain how you can locate the vertex, V, of the parabola with the given focus and directrix. Write the coordinates of the vertex.
















Part D
Which way will the parabola open? Explain.
















Part E
How can you find the value of p? Is the value of p for your parabola positive or negative? Explain.
















Part F
What is the value of p for your parabola?















Part G
Based on your responses to parts C and E above, write the equation of the parabola in vertex form. Show your work.















Part H
Construct the parabola using the parabola tool in GeoGebra. Take a screenshot of your work, save it, and insert the image below.
















Part I
Once you have constructed the parabola, use GeoGebra to display its equation. In the space below, rearrange the equation of the parabola shown in GeoGebra, and check whether it matches the equation in the vertex form that you wrote in part G. Show your work.
















Part J
To practice writing the equations of horizontal parabolas, write the equations of these two parabolas in vertex form:

focus at (4, 3), and directrix x = 2
focus at (2, -1), and directrix x = 8

Answer 1

Answers:

Part A

The directrix is a vertical line that is 8 units to the right of the focus F(-5, 2). So, we add 8 to the x-coordinate of the focus to get the equation of the directrix. The equation of a vertical line is of the form x = a, where a is the x-coordinate of any point on the line. So, the equation of the directrix is x = -5 + 8 = 3.

Part B

The line that is perpendicular to the directrix and passes through the focus is a horizontal line with the equation y = k, where k is the y-coordinate of the focus. So, the equation of the axis of symmetry is y = 2. The point of intersection, A, of the axis of symmetry and the directrix is the point where x = 3 and y = 2. So, A = (3, 2).

Part C

The vertex, V, of the parabola is the midpoint of the line segment from the focus to the directrix. Since the focus and the directrix are 8 units apart, the vertex is 4 units to the right of the focus. So, the coordinates of the vertex are V = (-5 + 4, 2) = (-1, 2).

Part D

The parabola will open to the right because the focus is to the left of the directrix.

Part E

The value of p is the distance from the vertex to the focus or the directrix. Since the vertex is 4 units to the right of the focus, p = 4. The value of p is positive when the parabola opens to the right and negative when it opens to the left. So, for this parabola, p is positive.

Part F

The value of p for this parabola is 4.

Part G

The vertex form of the equation of a horizontal parabola is
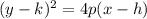`\( (y - k)^2 = 4p(x - h) \)`, where (h, k) is the vertex and p is the distance from the vertex to the focus. Substituting the coordinates of the vertex (-1, 2) and the value of p (4) into the equation, we get
`\( (y - 2)^2 = 4*4(x + 1) \), or \( (y - 2)^2 = 16(x + 1) \)`.

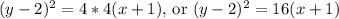Part H

*Look at Attachment*

Part I

*Look at Attachment*

Part J

1. For the parabola with focus at (4, 3) and directrix x = 2, the vertex is the midpoint between the focus and the directrix, which is (3, 3). The parabola opens to the right because the focus is to the right of the directrix, so p is positive. The distance from the vertex to the focus or the directrix is 1, so p = 1. The equation of the parabola is
`\( (y - 3)^2 = 4(x - 3) \)`.

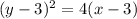2. For the parabola with focus at

The vertex of the parabola with focus at (2, -1) and directrix x = 8 is (5, -1). The parabola opens to the left because the focus is to the left of the directrix, so p is negative. The distance from the vertex to the focus or the directrix is 3, so p = -3. The equation of the parabola is
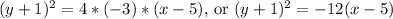`\( (y + 1)^2 = 4*(-3)*(x - 5) \), or \( (y + 1)^2 = -12(x - 5) \)`.