Question

in each case, find the linear combination of the first two vectors that is as close as possible to the third vector.

Answer 1

Part (a):

The linear combination of the first two vectors that is as close as possible to the third vector is given by the coefficients
`\(a \approx -0.0345\) and \(b \approx 1.2069\)`

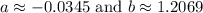
Part (b):

The coefficients for the linear combination are
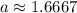`\(a \approx 1.6667\)` and
`\(b \approx 1.6667\)`.

Part (c):

The coefficients for the linear combination are
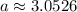`\(a \approx 3.0526\)` and
`\(b \approx 0.3158\)`.

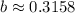Part (d):

The coefficients for the linear combination are
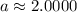`\(a \approx 2.0000\)` and
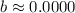`\(b \approx 0.0000\)` (rounded to four decimal places, and noting that the second coefficient is effectively zero).

Part (e):

The coefficients for the linear combination are
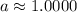`\(a \approx 1.0000\)` and
`\(b \approx 1.3333\)`.

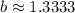The task involves finding a linear combination of two vectors that approximates a third vector. This can be interpreted as solving a system of equations where the coefficients of the linear combination are the variables we want to solve for.

Given vectors
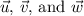`\(\vec{u}\), \(\vec{v}\), and \(\vec{w}\)`, we want to find scalars
`\(a\)` and
`\(b\)` such that the vector
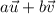`\(a\vec{u} + b\vec{v}\)` is as close as possible to
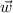`\(\vec{w}\)`. Mathematically, this is expressed as:

`\[ a\vec{u} + b\vec{v} \approx \vec{w} \]`

For example, in part (a), we have:

`\[ a[1, 2, 1] + b[2, 0, -1] \approx [3, -1, 0] \]`

To find the values of \(a\) and \(b\), we can set up a system of linear equations based on the components of the vectors. For (a), the system is:

`\[ a + 2b = 3 \]`

`\[ 2a + 0b = -1 \]`

`\[ a - b = 0 \]`

However, because this system might be overdetermined (more equations than unknowns), we typically solve it using methods like least squares, which finds the best approximation when an exact solution may not exist.

Let's start with part (a) and find the values of
`\(a\)`a and
`\(b\)`. We'll use the least squares method to find the best approximation.

For part (a):

The linear combination of the first two vectors that is as close as possible to the third vector is given by the coefficients
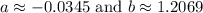`\(a \approx -0.0345\) and \(b \approx 1.2069\)` when rounded to four decimal places. The squared residual, which measures the discrepancy between the third vector and the linear combination of the first two, is approximately
`\(2.7931\)`.

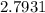This means that the vector
`\( -0.0345[1, 2, 1] + 1.2069[2, 0, -1] \)` will be the closest approximation to the vector
`\([3, -1, 0]\)` in a least squares sense.

Here are the solutions for the linear combinations that approximate the third vector for parts (b) through (e):

Part (b):

The coefficients for the linear combination are
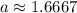`\(a \approx 1.6667\)` and
`\(b \approx 1.6667\)`.

Part (c):

The coefficients for the linear combination are
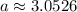`\(a \approx 3.0526\)` and
`\(b \approx 0.3158\)`.

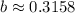Part (d):

The coefficients for the linear combination are
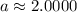`\(a \approx 2.0000\)` and
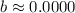`\(b \approx 0.0000\)` (rounded to four decimal places, and noting that the second coefficient is effectively zero).

Part (e):

The coefficients for the linear combination are
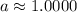`\(a \approx 1.0000\)` and
`\(b \approx 1.3333\)`.

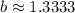the complete Question is given below: