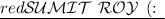Given:
Angle
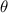 (angle between the ladder and the ground):
(angle between the ladder and the ground):
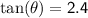
Distance between the foot of the ladder and the wall:
To find:
Length of the ladder:

Using the tangent function:
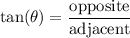
In this case:
Opposite side is the height of the wall:

Adjacent side is the distance between the foot of the ladder and the wall:
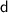
So we have:
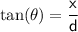
Substituting the given values:
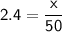
To find
 , we can solve for it by multiplying both sides of the equation by 50:
, we can solve for it by multiplying both sides of the equation by 50:
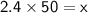
Simplifying:
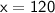
Therefore, the length of the ladder is 120 cm.
♥️