\dag \: \: \: \huge{ \boxed{ \sf{ \pink{Q\green{u \blue{e\color{yellow}s\red{ti\orange{on}}}}}}}} The areas of two similar triangles are 12cm2 and 48cm². If the height of the sm…

Question

asked Jun 12, 2024 86.9k views

1 Answer

Isabel Inc · Answer 1 · 2024-06-17T08:01:42+0000

$\dag \: \: \: \huge{ \boxed{ \sf{ \pink{A\green{N \blue{S\color{yellow}W\red{E\orange{R}}}}}}}}$

Given:

Area of the smaller triangle:
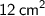
$\displaystyle\sf 12 \, cm^2$

Area of the larger triangle:
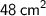
$\displaystyle\sf 48 \, cm^2$

Height of the smaller triangle:
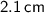
$\displaystyle\sf 2.1 \, cm$

Using the area ratio, we can set up the proportion:

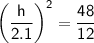
$\displaystyle\sf \left( (h)/(2.1) \right)^2 = (48)/(12)$

To find
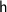$\displaystyle\sf h$ , we can solve the proportion above:

$\displaystyle\sf \left( (h)/(2.1) \right)^2 = 4$

Taking the square root of both sides:

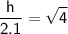
$\displaystyle\sf (h)/(2.1) = √(4)$

Simplifying the square root:

$\displaystyle\sf (h)/(2.1) = 2$

Cross-multiplying:

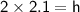
$\displaystyle\sf 2 * 2.1 = h$

Calculating the value:

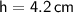
$\displaystyle\sf h = 4.2 \, cm$

Therefore, the corresponding height of the larger triangle is 4.2 cm.

$\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}$

♥️
$\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}$