Question

`\sf{\blue{«} \: \pink{ \large{ \underline{Q\orange{U} \red{E} \green{S} \purple{TI} \pink{{ON}}}}}}`

In ∆ABC, D and E are the points on the sides AB and AC respectively such that DE || BC. If AD = 6x – 7, DB = 4x – 3, AE = 3x – 3, and EC = 2x – 1 then find. the value of ‘x’.

no spam..!​

Answer 1

Explanation:

The basic proportionality theorem states that if a line is drawn parallel to one side of a triangle and it intersects the other two sides at two distinct points then it divides the two sides in the same ratio.

It is given that AD=4x−38, BD=3x−1, AE=8x−7 and CE=5x−3. Let AC=x

Using the basic proportionality theorem, we have

BD

AD

​

=

AC

AE

​

⇒

3x−1

4x−3

​

=

x

8x−5

​

⇒x(4x−3)=(3x−1)(8x−5)

⇒4x

2

−3x=3x(8x−5)−1(8x−5)

⇒4x

2

−3x=24x

2

−15x−8x+5

⇒4x

2

−3x=24x

2

−23x+5

⇒24x

2

−23x+5−4x

2

+3x=0

⇒20x

2

−20x+5=0

⇒5(4x

2

−4x+1)=0

⇒4x

2

−4x+1=0

⇒(2x)

2

−(2×2x×1)x+1

2

=0(∵(a−b)

2

=a

2

+b

2

−2ab)

⇒(2x−1)

2

=0

⇒(2x−1)=0

⇒2x=1

⇒x=

2

1

​

Hence, x=

2

1

​

.

Answer 2

`\sf{\blue{«} \: \pink{ \large{ \underline{A\orange{N} \red{S} \green{W} \purple{E} \pink{{R}}}}}}`

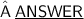
To find the value of 'x', we can use the property of parallel lines that states when a transversal intersects two parallel lines, the corresponding angles are equal.

In triangle ABC, we have DE parallel to BC. Therefore, we can conclude that triangle ADE is similar to triangle ABC.

Using the property of similar triangles, we can set up the following proportion:

`\displaystyle\sf (AD)/(DB) = (AE)/(EC)`

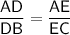
Substituting the given values:

`\displaystyle\sf (6x - 7)/(4x - 3) = (3x - 3)/(2x - 1)`

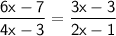
To solve this proportion for 'x', we can cross-multiply:

`\displaystyle\sf (6x - 7)(2x - 1) = (4x - 3)(3x - 3)`

Expanding both sides:

`\displaystyle\sf 12x^(2) - 6x - 14x + 7 = 12x^(2) - 9x - 12x + 9`

Combining like terms:

`\displaystyle\sf 12x^(2) - 20x + 7 = 12x^(2) - 21x + 9`

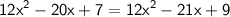
Moving all terms to one side:

`\displaystyle\sf 12x^(2) - 12x^(2) - 20x + 21x = 9 - 7`

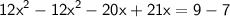
Simplifying:

`\displaystyle\sf x = 2`

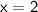
Therefore, the value of 'x' is 2.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`