Question

The linear magnification produced by a spherical mirror is +3. Analyse this value and state the (i) type of mirror and (ii) position of the object with respect to the pole of the mirror. Draw a ray diagram to show the formation of image in this case

answer in details!..​

Answer 1

The linear magnification produced by a spherical mirror is
`\displaystyle\sf +3`. Analyze this value and state the following:

(i) Type of mirror:

The sign of the magnification determines the type of mirror. Since the magnification is positive
`\displaystyle\sf (+3)`, it indicates that the mirror is a concave mirror.

(ii) Position of the object with respect to the pole of the mirror:

To determine the position of the object, we can use the magnification formula:

`\displaystyle\sf magnification=(-image\,height)/(object\,height)`

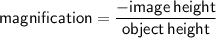
Since the magnification is given as
`\displaystyle\sf +3`, we can rewrite the formula as:

`\displaystyle\sf 3=(-image\,height)/(object\,height)`

Since the magnification is positive, the image height and object height must have opposite signs. Let's assume the object height is positive. Therefore, the image height must be negative.

Now, let's consider the case where the object is placed at a distance greater than the focal length (
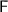`\displaystyle\sf F` ) from the pole of the concave mirror. In this scenario, the object is placed beyond the focal point (
`\displaystyle\sf F` ).

Using the mirror formula:

`\displaystyle\sf (1)/(f) =(1)/(v) -(1)/(u)`

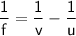
where
`\displaystyle\sf f` is the focal length,
`\displaystyle\sf v` is the image distance from the mirror, and
`\displaystyle\sf u` is the object distance from the mirror.

Since the object is beyond the focal point, the object distance
`\displaystyle\sf u` will be positive. Let's assume
`\displaystyle\sf u> 0`.

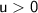Plugging the values into the mirror formula, we have:

`\displaystyle\sf (1)/(f) =(1)/(v) -(1)/(u)`

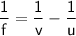
Since the magnification is given as
`\displaystyle\sf +3`, we know:

`\displaystyle\sf 3=(-v)/(u)`

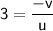
Rearranging the equation, we find:

`\displaystyle\sf v=(-u)/(3)`

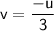
From the equation, we can see that the image distance
`\displaystyle\sf v` is negative, indicating that the image is formed on the same side as the object.

Therefore, for a concave mirror with a magnification of
`\displaystyle\sf +3` and an object placed beyond the focal point, the image will be formed on the same side as the object, and its height will be one-third of the object height.

Now, let's draw a ray diagram to visualize the formation of the image:

1. Draw the principal axis, which is a straight line passing through the center of curvature (
`\displaystyle\sf C`) and the pole (
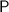`\displaystyle\sf P`) of the mirror.

2. Place the object (an arrow or an arrowhead) beyond the focal point, on the same side as the incident rays. Label the object as
`\displaystyle\sf AB`.

3. Draw a ray from the top of the object
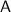`\displaystyle\sf A` parallel to the principal axis. After reflecting from the mirror, this ray will pass through the focal point
`\displaystyle\sf F`.

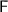4. Draw a ray from the top of the object
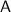`\displaystyle\sf A` towards the pole
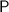`\displaystyle\sf P` of the mirror. After reflecting from the mirror, this ray will follow the path as if it came from the focal point
`\displaystyle\sf F`.

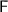5. The intersection point of the two reflected rays will give the top point
`\displaystyle\sf A'` of the image. Label the image as
`\displaystyle\sf A'B'`.

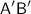6. Draw a perpendicular line from the top point
`\displaystyle\sf A'` to the principal axis. The bottom point
`\displaystyle\sf B'` of the image will be where this perpendicular line intersects the principal axis.

7. The image
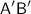`\displaystyle\sf A'B'` will be inverted (upside-down) and reduced in size compared to the object
`\displaystyle\sf AB`. The height of the image will be one-third the height of the object.

This ray diagram visually represents the formation of the image by a concave mirror with a linear magnification of
`\displaystyle\sf +3` when the object is placed beyond the focal point.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\underline{\textcolor{red}{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`