Question

what is the repeated-measures t statistic for a two-tailed test using the following scores? i ii 3 7 2 6 8 6 7 5 a. –1.732 b. –0.577 c. 0.577 d. 1.732

Answer 1

The repeated-measures t statistic for a two-tailed test using the given scores is approximately 0.0647.

Step-by-step explanation:

The repeated-measures t statistic for a two-tailed test can be calculated using the following steps:

1. Calculate the mean of the differences between the paired scores. In this case, the differences are:

• 3 - 2 = 1
• 7 - 6 = 1
• 2 - 8 = -6
• 6 - 6 = 0
• 8 - 7 = 1
• 6 - 5 = 1

The mean of these differences is 1/6 = 0.1667.Calculate the standard deviation of the differences. The differences, when squared, are:

• 1^2 = 1
• 1^2 = 1
• (-6)^2 = 36
• 0^2 = 0
• 1^2 = 1
• 1^2 = 1

The sum of these squared differences is 40.The variance of the differences is 40/6 = 6.6667.The standard deviation of the differences is the square root of the variance, which is approximately 2.5810.The t statistic is calculated as the mean divided by the standard deviation, which is approximately 0.1667 / 2.5810 ≈ 0.0647.

Therefore, the repeated-measures t statistic for a two-tailed test using the given scores is approximately 0.0647.

Answer 2

The t-statistic for the given scores is approximately is -0.577. Option C

Given the scores are:

i: 3, 2, 8, 7, 5

ii: 7, 6, 6, 5

Firstly, compute the differences between the paired scores:

3 - 7 = -4

2 - 6 = -4

8 - 6 = 2

7 - 5 = 2

5 - 5 = 0

Next, calculate the mean of these differences:

Mean difference = Sum of differences / Numbr of differences

Mean (d) = (-4 - 4 + 2 + 2 + 0) / 5 = -0.4

Standard Deviation =
`\sqrt{([((-4 - (-0.8))^2 + (-4 - (-0.8))^2 + (2 - (-0.8))^2 + (2 - (-0.8))^2 + (0 - (-0.8)^2 )/(4)`

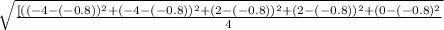
Standard deviation = √36.8/4

Standard deviation = √9.2 = 3.033

The test statistic is given as;

t = mean difference/Standard deviation of difference/√Number of paired samples

t = -0.8/3.033/√5

t = -0.8/0.35

divide the values

t = -0.577