Question

Select the correct answer.
What is the domain of y= tan x?

Answer 1

Explanation:

For some problems, stating the domain actually means to identify what x CANNOT be as opposed to what x IS. This occurs with tangent and cotangent functions along with rational functions.

As far as the tangent function goes, look at your unit circle. Your unit circle gives you 2 values for each angle, the first value reflects the cosine of the angle and the second value reflects the sine of the angle. This is because cosine is directly related to the x values and sine is directly related to the y values; cos goes into the "x" position and sin goes into the "y" position inside the brackets just like x and y go into parenthesis for coordinates. Anyway, a ratio is undefined if the denominator equals 0, right? And since tangent is the same as sin/cos, tangent is undefined when cos is 0. This occurs at
`(\pi)/(2)+k\pi` . That means that tangent does NOT exist at pi over 2 and every integer of pi you add in after. Let's look at a couple of examples of how that domain "works". Adding in an integer means adding in 1, 2, 3, etc. If the domain of tangent is undefined at
`(\pi)/(2)+k\pi`, then let's let k = 1, and

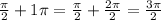`(\pi)/(2)+1\pi=(\pi)/(2)+(2\pi)/(2)=(3\pi)/(2)` . Now let k = 2:

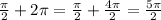`(\pi)/(2)+2\pi=(\pi)/(2)+(4\pi)/(2)=(5\pi)/(2)`. Now let k = 3:

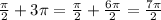`(\pi)/(2)+ 3\pi=(\pi)/(2)+(6\pi)/(2)=(7\pi)/(2)`. And it continues like that.

You can see when you graph the tangent function in radian mode on your calculator that these values where tangent is undefined show up as asymptotes. Use your unit circle and your graphs to determine the domain of trig functions.

Answer 2

π/2 + n*π

Explanation:

All real numbers except π/2 + n*π