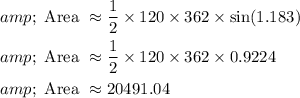Question

a cat runs due east 120 feet to a corner. after turning through an angle of 67.8, the cat walks 362 feet to the second corner. then the cat walks back to the starting point, what is the area of the triangle formed by his path

Answer 1

The area of the triangle formed by the cat's path is approximately 20490 square feet.

To find the area of the triangle formed by the cat's path, you can use the formula for the area of a triangle given two sides and the included angle. The formula is:

Area

`\text { Area }=(1)/(2) a b \sin (C)`

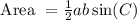
where a and b are the lengths of two sides of the triangle, and C is the included angle between those sides.

Let's label the sides of the triangle formed by the cat's path:

AB is the first segment where the cat runs due east for 120 feet.

BC is the second segment where the cat turns through an angle of 67.8° and walks 362 feet.

CA is the third segment where the cat walks back to the starting point.

Now, let's substitute the given values into the formula:

`\text { Area }=(1)/(2) * 120 * 362 * \sin \left(67.8^(\circ)\right)`

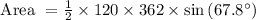
First, convert the angle from degrees to radians because trigonometric functions in most programming languages use
`1^(\circ)=(\pi)/(180)` radians.

`\text { Area }=(1)/(2) * 120 * 362 * \sin \left(67.8^(\circ) * (\pi)/(180)\right)`

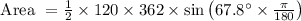
Now, calculate the value:

`\begin{aligned}& \text { Area } \approx (1)/(2) * 120 * 362 * \sin (1.183) \\& \text { Area } \approx (1)/(2) * 120 * 362 * 0.9224 \\& \text { Area } \approx 20491.04\end{aligned}`

Answer 2

The area of the triangle formed by his path is 20490ft²

The area of a triangle is expressed as;

A = 1/2bh

where b is the base and h is the height.

We need to find the vertical height of the triangle formula.

Using Pythagorean theorem

vertical height = √ 362² - 120²

= √ 116644

= 341.5 ft

Using area of triangle now

A = 1/2 × 341.5 × 120

A= 20490 ft²

Therefore, the area of triangle formed by his path is 20490ft²