Question

Explain how factoring is used when adding or subtracting rational expressions. Include an example in your explanation.

Answer 1

Refer to the step-by-step explanation.

Explanation:

When adding or subtracting rational expressions, factoring plays a crucial role in simplifying the expressions and finding a common denominator. Factoring involves breaking down an expression into its constituent factors. This allows us to identify common factors and perform simplifications.

Let's consider an example to illustrate how factoring is used when adding or subtracting rational expressions:

`\hrulefill`

Example:

Simplify the expression,

`(3x + 4)/(x^2 - 1) + (2x - 1)/(x^2 + 3x + 2)`

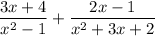
Step 1: Factor the denominators:

The denominator of the first expression, x² - 1, is a difference of squares and can be factored as (x - 1)(x + 1).

The denominator of the second expression, x² + 3x + 2, can be factored as (x + 1)(x + 2).

`\Longrightarrow (3x + 4)/((x-1)(x+1)) + (2x - 1)/((x+1)(x+2))`

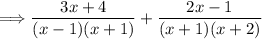
Step 2: Determine the common denominator:

To find the common denominator, we need consider the factored forms of the denominators and take the product of all the unique factors. In this case, the common denominator is (x - 1)(x + 1)(x + 2).

Step 3: Adjust the numerators:

We need to adjust the numerators of the rational expressions to have the same denominator. To do this, we multiply the numerator and denominator of each expression by the missing factors.

`\Longrightarrow (3x + 4)/((x-1)(x+1)) \cdot ((x+2))/((x+2)) + (2x - 1)/((x+1)(x+2))\cdot ((x-1))/((x-1))\\\\\\\\`

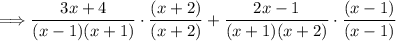
Step 4: Combine the expressions:

Now that both expressions have the same denominator, we can add or subtract the numerators while keeping the denominator unchanged. In this case, we are adding the expressions, so we have:

`\Longrightarrow ((3x + 4)(x+2)+(2x-1)(x-1))/((x-1)(x+1)(x+2))`

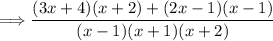
Step 5: Simplify, if possible:

We can simplify the numerator by expanding and combining like terms:

`\Longrightarrow ((3x^2+10x+8)+(2x^2-3x+1))/((x-1)(x+1)(x+2))\\\\\\\\`

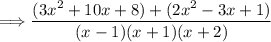
Simplifying further:

`\Longrightarrow (5x^2+7x+9)/((x-1)(x+1)(x+2))`

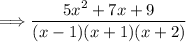
Thus, the resulting expression is found.

`\boxed{\boxed{ (5x^2+7x+9)/((x-1)(x+1)(x+2))}}`

By factoring the denominators, we were able to find the common denominator and combine the expressions into a single fraction. Factoring simplifies the process by breaking down complex expressions into manageable factors, allowing us to perform arithmetic operations with rational expressions more easily.