Question

What is the sum of the first seven terms of the geometric series? 3 12 48 192 ...

Answer 1

16373

Explanation:

Pre-Solving

We are given the following geometric series:

3, 12, 48, 192....

And we want to find the sum of 7 terms.

The sum of n number of terms in a geometric series is
`S_n=(t_1(1-r^n))/(1-r)`, where
`t_1` is the first term, r is the common ratio, and n is the number of terms being added.

To get the common ratio, we can divide
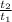`(t_2)/(t_1)`; as we already know,
`t_1` is the first term, which is 3.
`t_2` is the second term, which is 12.

So, the common ratio is 12/3 = 4

Since we are finding the sum of the first seven terms, n = 7.

Solving

We can plug what we know into the formula.

`S_n=(t_1(1-r^n))/(1-r)`

`S_7=(3(1-4^7))/(1-4)`

Plug the above into a calculator.

`S_7 = 16383`

So, the sum is 16383.