Question

a curve with a radius of 50 m is banked at an angle of 25˚. the coefficient of static friction between the tires and the roadway is 0.3

Answer 1

For a curve with a 50 m radius banked at 25˚ and a coefficient of static friction of 0.3, the speed of the vehicle to avoid sliding is approximately 25.2 m/s.

Step-by-step explanation:

To find the speed, we use the equation
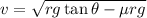`\( v = √(rg\tan\theta - \mu rg) \)`, where r is the radius, g is the acceleration due to gravity,
`\( \theta \)` is the banking angle, and
`\( \mu \)` is the coefficient of static friction. Plugging in the given values, we calculate the minimum speed required to prevent sliding on the banked curve. In this scenario, the banking angle and the coefficient of static friction work together to provide the necessary centripetal force, allowing the vehicle to negotiate the curve without slipping.

The physics of banked curves and the factors influencing the minimum speed required to prevent sliding, including the role of friction and banking angles. Understanding these principles is crucial for designing safe roadways and analyzing vehicle dynamics.

Answer 2

The minimum coefficient of friction needed for a car to negotiate an unbanked 50.0 m radius curve at 30.0 m/s is approximately 0.167.

Step-by-step explanation:

Physics: Friction and Banked Curves

When a car goes around a curve, friction between the tires and the road prevents it from sliding off the curve. In the case of an unbanked curve, where the road is flat, the minimum coefficient of friction needed to negotiate a curve can be calculated using the centripetal force formula. For a car to negotiate a 50.0 m radius unbanked curve at 30.0 m/s, the minimum coefficient of friction needed is approximately 0.167.