Question

What is the equation of a line that passes through the points (0,6) and (2,10)?

Answer 1

y = 2x + 6

Explanation:

To find the equation of a line that passes through two points, you can use the slope-intercept form of a linear equation: y = mx + b, where m represents the slope and b represents the y-intercept.

First, let's find the slope (m) using the given points (0,6) and (2,10):

m = (
`y_{2` -
`y_{1`) / (
`x_{2` -
`x_{1`)

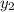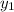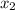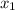m = (10 - 6) / (2 - 0)

m = 4 / 2

m = 2

Now that we have the slope (m = 2), we can substitute one of the points and the slope into the slope-intercept form to find the y-intercept (b). Let's use the point (0,6):

y = mx + b

6 = 2(0) + b

6 = 0 + b

b = 6

So, the y-intercept (b) is 6.

Therefore, the equation of the line that passes through the points (0,6) and (2,10) is:

y = 2x + 6