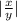Question

Please anyone that can help me

Answer 1

`|(x)/(y) |`

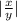
Explanation:

Pre-Solving

We are given the following expression:
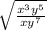`\sqrt(x^3y^5)/(xy^7)`, where x > 0 and y > 0.

We want to simplify it.

To do that, we can first simplify what is under the radical, then take the square root of what is left.

Recall that when simplifying exponents, we don't want any negative or non-integer radicals left.

Solving

To simplify what is under the radical, we can remember the rule where
`(a^n)/(a^m) = a^(n-m)`.

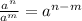So, that means that
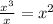`(x^3)/(x) = x^2` and
`(y^5)/(y^7) = y^(-2)` .

Under the radical, we now have:

`\sqrt{x^2y^(-2)}`

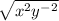
Now, we take the square root of both exponents to get:

`|xy^(-1)|`

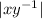
The reason why we need the absolute value signs is because we know that x > 0 and y > 0, but when we take the square root of of
`x^2` and
`y^(-2)` , the values of x and y can be either positive or negative, so by taking the absolute value, we ensure that the value is positive.

However, we aren't done yet; remember that we don't want any radicals to be negative, and the integer of y is negative.

Recall that if
`a^(-n)`, that is equal to
`(1)/(a^n)`.

So, by using that,

`|x * (1)/(y) |`

This can be simplified to:

`|(x)/(y) |`