Answer:
Approximately
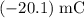 .
.
Step-by-step explanation:
By Coulomb's Law, at a distance of
 from an electric charge
from an electric charge
 , the electric potential resulting from that charge would be:
, the electric potential resulting from that charge would be:
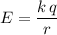 ,
,
Where
 is Coulomb's Constant.
is Coulomb's Constant.
When there are more than one electric charges nearby, the resultant electric potential is the scalar sum of the potential from each of these charges.
Let
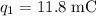 denote the two charges at adjacent vertices of this square. Let
denote the two charges at adjacent vertices of this square. Let
 denote the unknown charge.
denote the unknown charge.
Let
 denote the length of each side of this square. At the empty vertex:
denote the length of each side of this square. At the empty vertex:
- Distance from one of the
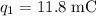 charge would be
charge would be
 ;
; - Distance from the other
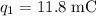 charge would be
charge would be
 (along the diagonal of the square.)
(along the diagonal of the square.) - Distance from the unknown charge
 would be
would be
 .
.
The resultant electric potential at the empty vertex would be the sum of the potential from each of these charges:
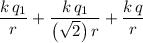 .
.
Set this expression value to
 and solve for
and solve for
 .
.
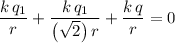 .
.
Note that
 and
and
 are both non-zero constants and can be eliminated. Hence:
are both non-zero constants and can be eliminated. Hence:
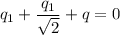 .
.
 .
.
In other words, the unknown charge should be
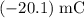 to ensure that the electric potential is zero at the empty vertex.
to ensure that the electric potential is zero at the empty vertex.