Question

Please help me. i need urgent help

Answer 1

Explanation:

I think there is a typo in the question

Qn : let p(n) be
`\sum\limits^n_(i = 1){i2^i} = 2 + (n-1)2^(n+1) \;\;\;\;\;\;:n\geq 1`

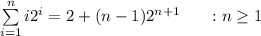
When n = 1:

LHS: 1(2¹) = 2

RHS: 2 + (1 - 1)(2¹ ⁺ ¹) = 2

LHS = RHS

⇒ p(n) holds for n = 1

Let us assume that the proof holds for p(n): n = x

ie.

`p(x): \sum\limits^x_(i = 1){i2^i} = 2 + (x-1)2^(x+1)`

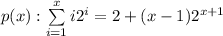
To prove that the proof holds for n = x+1

ie
`p(x+1): \sum\limits^(x+1)_(i = 1){i2^i} = 2 + (x)2^(x+2)`

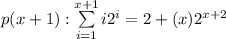
Consider LHS

`\sum\limits^(x+1)_(i = 1){i2^i}\\\\= \sum\limits^(x)_(i = 1){i2^i}+\sum\limits^(x+1)_(i = x+1){i2^i}\\\\= p(x) + (x+1)2^(x+1)\\\\= 2 + (x-1)2^(x+1) + (x+1)2^(x+1)\\\\= 2 + 2^(x+1) (x-1 + x+1)\\\\= 2 + 2^(x+1) (2x)\\\\= 2 + (x)2^(x+2)\\\\= RHS`