Question

Use trigonometric identities to verify each expression is equal.

(sin(x))/(1-cos(x)) - cot(x) = csc(x)

Answer 1

Explanation:

`(sin(x))/(1-cos(x)) -cot(x)=csc(x)\\`

`(sin(x))/(1-cos(x)) -(cos(x))/(sin(x)) =csc(x)`

`(sin^(2)(x)-cos(x)+cos^(2)(x) )/((1-cos(x))sin(x)) =csc(x)\\\\(1-cos(x))/((1-cos(x))sin(x)) =csc(x)\\`

`(1)/(sin(x)) =csc(x)\\csc(x)=csc(x)`

QED

Answer 2

See below for proof.

Explanation:

Use the cotangent identity to rewrite cot(x) as cos(x) / sin(x):

`(\sin(x))/(1-\cos(x))-\cot(x)=(\sin(x))/(1-\cos(x))-(\cos (x))/(\sin(x))`

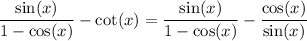
Make the denominators of both fractions the same:

`=(\sin(x))/(1-\cos(x))\cdot{(\sin(x))/(\sin(x))-(\cos (x))/(\sin(x))\cdot{(1-\cos(x))/(1-\cos(x))`

`=(\sin^2(x))/(\sin(x)(1-\cos(x)))-(\cos (x)(1-\cos(x)))/(\sin(x)(1-\cos(x)))`

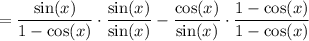
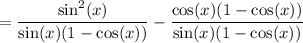
Expand the numerator of the second fraction:

`=(\sin^2(x))/(\sin(x)(1-\cos(x)))-(\cos (x)-\cos^2(x))/(\sin(x)(1-\cos(x)))`

`\textsf{Apply the fraction rule} \quad (a)/(c)-(b)/(c)=(a-b)/(c):`

`=(\sin^2(x)-(\cos (x)-\cos^2(x)))/(\sin(x)(1-\cos(x)))`

`=(\sin^2(x)-\cos (x)+\cos^2(x))/(\sin(x)(1-\cos(x)))`

`=(\sin^2(x)+\cos^2(x)-\cos (x))/(\sin(x)(1-\cos(x)))`

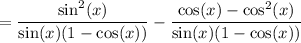
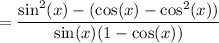
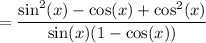
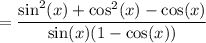
Apply the trigonometric identity, sin²θ + cos²θ = 1, to the numerator:

`=(1-\cos (x))/(\sin(x)(1-\cos(x)))`

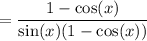
Factor out the common term (1 - cos(x)) from the numerator and denominator:

`=(1)/(\sin(x))`

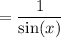
Finally, use the cosecant identity, csc(x) = 1 / sin(x):

`=\csc(x)`

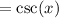
Hence we have verified that the left side of the equation equals the right side.