Question

Help with the remaining one please!!

Answer 1

`h'(1)=4\sec^2(8)`

`h''(1)=32\sec^2(8)\tan(8)`

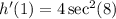
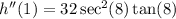
Explanation:

Given the following function.

`h(x)=\tan(4x+4)`

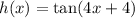
Find the following:

`h'(1)= \ ??\\\\h''(1)= \ ??\\\\\\\hrule`

Taking the first derivative of h(x). We will use the chain rule and the rule for tangent.

`\boxed{\left\begin{array}{ccc}\text{\underline{The Chain Rule:}}\\\\(d)/(dx)[f(g(x))]=f'(g(x)) \cdot g'(x) \end{array}\right}\\\\\\\boxed{\left\begin{array}{ccc}\text{\underline{The Tangent Rule:}}\\\\(d)/(dx)[\tan(x)]=\sec^2(x) \end{array}\right}`

`h(x)=\tan(4x+4)\\\\\\\Longrightarrow h'(x)=\sec^2(4x+4) \cdot4\\\\\\\therefore \boxed{h'(x)=4\sec^2(4x+4)}`

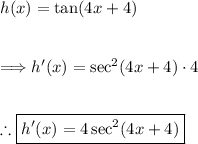
Now plugging in x=1:

`\Longrightarrow h'(1)=4\sec^2(4(1)+4)\\\\\\\Longrightarrow \boxed{\boxed{h'(1)=4\sec^2(8)}}`

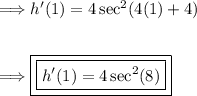
Taking the second derivative of h(x). Using the chain rule again and the secant rule.

`\boxed{\left\begin{array}{ccc}\text{\underline{The Secant Rule:}}\\\\(d)/(dx)[\sec(x)]=\sec(x) \tan(x) \end{array}\right}`

`h'(x)=4\sec^2(4x+4)\\\\\\\Longrightarrow h''(x)=(4\cdot 2)\sec(4x+4) \cdot \sec(4x+4)\tan(4x+4) \cdot 4\\\\\\\therefore \boxed{h''(x)=32\sec^2(4x+4)\tan(4x+4)}`

Now plugging in x=1:

`\Longrightarrow h''(1)=32\sec^2(4(1)+4)\tan(4(1)+4)\\\\\\\therefore \boxed{\boxed{ h''(1)=32\sec^2(8)\tan(8)}}`

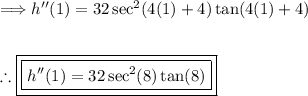
Thus, the problem is solved.