Question

Please assist quickly! Any unnecessary answers will be reported!

Triangle A'B'C' s the result of dilating ABC about point B by a scale factor of 4/3.

Determine whether each claim about the properties of ABC and A'B'C is true or false.

The measures of C and C' is equal.
The coordiante of C and C' are the same.

Answer 1

`\textsf{The\;measures\;of\;$\angle C$\;and\;$\angle C'$\;are\;equal.\;\;$\boxed{\sf True}$}`

`\textsf{The\;coordinates\;of\;$C$\;and\;$C'$\;are\;the\;same.\;\;$\boxed{\sf False}$}`

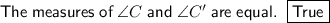
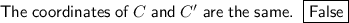
Explanation:

Dilation is a geometric transformation that resizes an object without altering its shape or proportions. It is typically performed with respect to a fixed center point called the center of dilation

The scale factor determines the amount by which the object is magnified or reduced. If the scale factor is greater than 1, the object is enlarged, whereas if it is between 0 and 1, the object is reduced.

Dilations generate similar figures by maintaining the same shape and angle measures while creating proportional sides through multiplication by the scale factor.

As triangle A'B'C' is a dilation of triangle ABC, they are similar triangles. This means that the measures of the interior angles of the original triangle ABC will be preserved in the dilated triangle A'B'C'. Therefore, the measures of ∠C and ∠C' are equal.

As the center of dilation is point B of triangle ABC, and the center of dilation is fixed, this means that point B and point B' will be the same. Points A' and C' will be different from points A and C, as sides B'C' and B'A' are longer than sides BC and BA due to ΔA'B'C' being a dilation of ΔABC. Therefore, the coordinates of C and C' are not the same.