Question

Which equation represents the line that is perpendicular to y=4/5x + 23 and passes through (-40,20)?

Answer 1

y =
`(-5)/(4)`x - 30

Explanation:

we will use the x = -40 and the y = 20 from the point given (-40,20). The perpendicular slope would be the opposite reciprocal from the slope given. The slope given is 4/5. The reciprocal is 5/4 and the opposite would be -5/4

y = mx + b Plug in what we know and solve for b

20 =
`(-5)/(4)` ( -40) + b

20 =
`(-5)/(4)` ·
`(-40)/(1)` + b

20 =
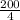`(200)/(4)` + b

20 = 50 + b Subtract 50 from both sides

20 - 50 = 50 - 50 + b

-30 = b

To write the equation we need the slope (m) (
`(-5)/(4)`) and the y-intercept (b) (-30)

y = mx + b

y =
`(-5)/(4)`x - 30

Helping in the name of Jesus.