Question

Please find the result !​

Answer 1

`\displaystyle - (1)/(2)`

Explanation:

we would like to compute the following limit:

`\displaystyle \lim _(x \to 0) \left( \frac{1}{ \ln(x + \sqrt{ {x}^(2) + 1} ) } - (1)/( \ln(x + 1) ) \right)`

if we substitute 0 directly we would end up with:

`\displaystyle(1)/(0) - (1)/(0)`

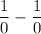
which is an indeterminate form! therefore we need an alternate way to compute the limit to do so simplify the expression and that yields:

`\displaystyle \lim _(x \to 0) \left( \frac{ \ln(x + 1) - \ln(x + \sqrt{ {x}^(2) + 1 } }{ \ln(x + \sqrt{ {x}^(2) + 1} ) \ln(x + 1) } \right)`

now notice that after simplifying we ended up with a rational expression in that case to compute the limit we can consider using L'hopital rule which states that

`\rm \displaystyle \lim _(x \to c) \left( (f(x))/(g(x)) \right) = \lim _(x \to c) \left( (f'(x))/(g'(x)) \right)`

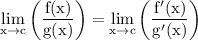
thus apply L'hopital rule which yields:

`\displaystyle \lim _(x \to 0) \left( \frac{ (d)/(dx) \ln(x + 1) - \ln(x + \sqrt{ {x}^(2) + 1 } }{ (d)/(dx) \ln(x + \sqrt{ {x}^(2) + 1} ) \ln(x + 1) } \right)`

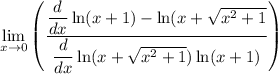
use difference and Product derivation rule to differentiate the numerator and the denominator respectively which yields:

`\displaystyle \lim _(x \to 0) \left( \frac{ (1)/(x + 1) - (1)/( √(x + 1) ) }{ \frac{ \ln(x + 1)}{ \sqrt{ {x}^(2) + 1 } } + \frac{ \ln(x + \sqrt{x ^(2) + 1 } }{x + 1} } \right)`

simplify which yields:

`\displaystyle \lim _(x \to 0) \left( \frac{ \sqrt{ {x}^(2) + 1 } - x - 1 }{ (x + 1)\ln(x + 1 ) + \sqrt{ {x}^(2) + 1} \ln( x + \sqrt{ {x }^(2) + 1} ) } \right)`

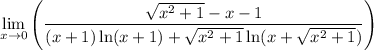
unfortunately! it's still an indeterminate form if we substitute 0 for x therefore apply L'hopital rule once again which yields:

`\displaystyle \lim _(x \to 0) \left( \frac{ (d)/(dx) \sqrt{ {x}^(2) + 1 } - x - 1 }{ (d)/(dx) (x + 1)\ln(x + 1 ) + \sqrt{ {x}^(2) + 1} \ln( x + \sqrt{ {x }^(2) + 1} ) } \right)`

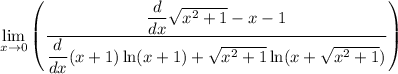
use difference and sum derivation rule to differentiate the numerator and the denominator respectively and that is yields:

`\displaystyle \lim _(x \to 0) \left( \frac{ \frac{x}{ \sqrt{ {x}^(2) + 1 } } - 1}{ \ln(x + 1) + 2 + \frac{x \ln(x + \sqrt{ {x}^(2) + 1 } ) }{ \sqrt{ {x}^(2) + 1 } } } \right)`

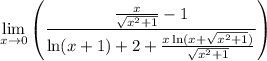
thank god! now it's not an indeterminate form if we substitute 0 for x thus do so which yields:

`\displaystyle \frac{ \frac{0}{ \sqrt{ {0}^(2) + 1 } } - 1}{ \ln(0 + 1) + 2 + \frac{0 \ln(0 + \sqrt{ {0}^(2) + 1 } ) }{ \sqrt{ {0}^(2) + 1 } } }`

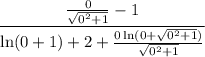
simplify which yields:

`\displaystyle - (1)/(2)`

finally, we are done!

Answer 2

9514 1404 393

Answer:

-1/2

Explanation:

Evaluating the expression directly at x=0 gives ...

`(1)/(\ln(√(1)))-(1)/(\ln(1))=(1)/(0)-(1)/(0)\qquad\text{an indeterminate form}`

Using the linear approximations of the log and root functions, we can put this in a form that can be evaluated at x=0.

The approximations of interest are ...

`\ln(x+1)\approx x\quad\text{for x near 0}\\\\√(x+1)\approx (x)/(2)+1\quad\text{for x near 0}`

__

Then as x nears zero, the limit we seek is reasonably approximated by the limit ...

`\displaystyle\lim_(x\to0)\left((1)/(x+(x^2)/(2))-(1)/(x)\right)=\lim_(x\to0)\left((x-(x+(x^2)/(2)))/(x(x+(x^2)/(2)))\right)\\\\=\lim_(x\to0)(-(x^2)/(2))/(x^2(1+(x)/(2)))=\lim_(x\to0)(-1)/(2+x)=\boxed{-(1)/(2)}`

_____

I find a graphing calculator can often give a good clue as to the limit of a function.