Question

Solve using elimination

Answer 1

(1/2, -1/2)

Explanation:

Solving the given system of equations using elimination.

(1) - Write down the system of equations.

`\left\{\begin{array}{c}(1)/(2)x-(1)/(3)y=(5)/(12)\\\\(5)/(6)x+(1)/(2)y=(1)/(6)\end{array}\right`

(2) - Choose one variable to eliminate by multiplying one or both equations by appropriate constants. The goal is to make the coefficients of one variable in both equations equal or multiples of each other.

Let's eliminate the "y" variable in this example. Multiply Equation 1 by 3/2:

`\Longrightarrow \left\{\begin{array}{c}(3)/(2) \cdot\Big[(1)/(2)x-(1)/(3)y=(5)/(12)\Big]\\\\(5)/(6)x+(1)/(2)y=(1)/(6)\end{array}\right\\\\\\\\\Longrightarrow \left\{\begin{array}{c}\Big((3)/(2) \cdot (1)/(2)\Big)x-}\Big((3)/(2) \cdot (1)/(3)\Big)y=}(3)/(2) \cdot (5)/(12)\\\\(5)/(6)x+(1)/(2)y=(1)/(6)\end{array}\right`

`\Longrightarrow\left\{\begin{array}{c}(3)/(4)x-(1)/(2)y=(5)/(8)\\\\(5)/(6)x+(1)/(2)y=(1)/(6)\end{array}\right`

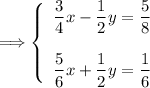
(3) - Add or subtract the modified equations to eliminate the chosen variable.

In this case, we'll add equations 1 and 2:

`\Big[(3)/(4)x-(1)/(2)y=(5)/(8)\Big]+ \Big[(5)/(6)x+(1)/(2)y=(1)/(6) \Big] = \Big((3)/(4)x+(5)/(6)x\Big)+\Big(-(1)/(2)y+(1)/(2)y\Big)=\Big((5)/(8)+(1)/(6)\Big)\\\\\\\Longrightarrow (19)/(12)x=(19)/(24)`

(4) - Solve the resulting equation for the remaining variable.

In this case, solve for "x":

`(19)/(12)x=(19)/(24)\\\\\\\Longrightarrow x=(19)/(24) \cdot (12)/(19)\\\\\\\Longrightarrow x=(228)/(456)\\\\\\\therefore \boxed{x=(1)/(2) }`

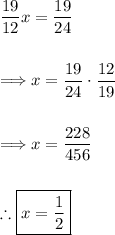
(5) - Substitute the value of "x" back into one of the original equations and solve for the remaining variable.

Let's use Equation 1:

`(1)/(2)x-(1)/(3)y=(5)/(12); \ x=\frac12\\\\\\\Longrightarrow (1)/(2)\Big((1)/(2)\Big)-(1)/(3)y=(5)/(12)\\\\\\\Longrightarrow (1)/(4)\Big-(1)/(3)y=(5)/(12)\\\\\\\Longrightarrow -(1)/(3)y=(5)/(12)-(1)/(4) \\\\\\\Longrightarrow -(1)/(3)y=(1)/(6)\\\\\\\Longrightarrow y=(1)/(6) \cdot -3\\\\\\\therefore \boxed{y=-\frac12}`

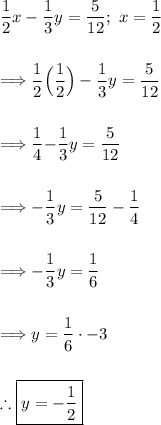
Therefore the solution to the system is (1/2, -1/2).