Question

PLEASE HELP!
Thanks in advance!​

Answer 1

10.67 degree.

Explanation:

Note:
The angle between two lines can be found using their direction cosines. The formula is:

`\boxed *`

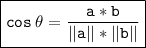
where:

• a and b are the direction cosines of the two lines
• 
  `\theta` is the angle between the two lines
• ||a|| and ||b|| are the magnitudes of a and b

In this case, the direction cosines of the two lines are proportional to 1, 2, 3 and 3, 4, 5.

So, we can write the direction cosines as follows:

a = (1, 2, 3)

b = (3, 4, 5)

The magnitudes of a and b are:

`\tt ||a|| = √(1^2 + 2^2 + 3^2) = √(13)`

`\tt ||b|| = √(3^2 + 4^2 + 5^2)= 5√(2)`

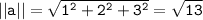
Now, we can find the angle between the two lines using the formula above:

`\tt cos \: \theta = (1 * 3 + 2 * 4 + 3 * 5)/(√(13) * 5√(2) )=(13√(7))/(35)`

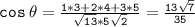
The angle theta can be found using the arc cos function or inverse cos function.

`\tt \theta =cos^(-1)((13√(7))/(35))=10.67`

Therefore, the angle between the two lines is 10.67 degree.