Question

Which statements apply to the expression (three-fifths) cubed? Check all that apply.

The base is Three-fifths.
The base is 3.
The exponent is 3.
The expanded form is Three-fifths times three-fifths times three-fifths.
The expanded form is StartFraction 3 times 3 times 3 Over 5 EndFraction.
(Three-fifths) cubed = StartFraction 9 Over 15 EndFraction

Answer 1

The true statements are:

below in bold

Work/explanation:

The statements which apply to the given scenario are the following:

The base is Three-fifths.

The expanded form is three-fifths times three-fifths times three-fifths.

The exponent is 3.

Let's take a closer look at the expression
`\sf{\bigg((3)/(5)\bigg)^3}`.

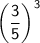What is the base and what is the exponent?

Think of the expression
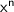`\sf{x^n}`. Here, x is the base, and n is the exponent.

Similarly, with our exercise here, 3/5 is the base and 3 is the exponent.

`\rule{350}{4}`

Now, what is the expanded form of the expression? If we have something cubed, what does it mean?

It means that this something is multiplied by itself 3 times.

So the expanded form is three-fifths times three-fifths times three-fifths.

Finally, when we raise a fraction to a power, we raise both the numerator and the denominator to that power.