Question

-60x^4+54x factor completely

Answer 1

The answer is:

`\sf{-6x(10x^3+9)}`

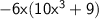
Work/explanation:

What does it mean to factor completely?

To factor an expression completely, we find its GCF, and factor it out.

Let's do it with the expression we have here:
`\sf{-60x^4+54x}`.

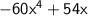I begin by finding the GCF. In this case, the GCF is 6x.

Next, I divide each term by -6x:

`\sf{-60x^4/-6x=\bf{10x^3}`

`\sf{54x/-6x=9}`

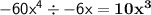
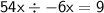
I end up with:

`\sf{-6x(10x^3+9)}`

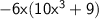
Hence, the factored expression is
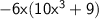`\sf{-6x(10x^3+9)}`.