Question

A person jogs 780 meters south and then 360 meters west. What is the direction of the person's resultant vector? Hint: Draw a vector diagram. Ө 0 = [ ? ]° Round your answer to the nearest hundredth.

Answer 1

245.22° (nearest hundredth)

Explanation:

To calculate the direction of the jogger's resultant vector, we can draw a vector diagram (see attachment).

• The starting point of the person is the origin (0, 0).
• Given the jogger first jogs 780 m south, draw a vector from the origin south along the y-axis and label it 780 m.
• Given the jogger then jogs 360 m west, draw a vector from the terminal point of the previous vector in the west direction (to the left) and label it 360 m.

Since the two vectors form a right angle, we can use the tangent trigonometric ratio.

`\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$ \tan x=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $x$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}`

The resultant vector is in quadrant III, since the person jogs south (negative y-direction) and then west (negative x-direction).

As the direction of a resultant vector is measured in an anticlockwise direction from the positive x-axis, we need to subtract the angle found using the tan ratio from 270°.

The angle between the y-axis and the resultant vector can be found using tan x = 360 / 780. Therefore, the expression for the direction of the resultant vector θ is:

`\theta=270^(\circ)+\arctan \left((360)/(780)\right)`

`\theta=270^(\circ)-24.7751405...^(\circ)`

`\theta=245.22^(\circ)\; \sf (nearest\;hundredth)`

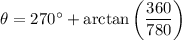
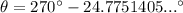
Therefore, the direction of the plane's resultant vector is approximately 245.22° (measured anticlockwise from the positive x-axis).