Question

polly is pushing a box across the floor with a force of 30 n. the force of gravity is –8 n, and the normal force is 8 n. which value could describe the force of friction if polly could not move the box? –30 n –8 n 8 n 30 n

Answer 1

`(-30)\; {\rm N}`.

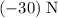Step-by-step explanation:

Given that the box isn't moving, acceleration of the box would be
`0`. By Newton's Laws of Motion, the resultant force on the box would be
`0\; {\rm N}` in all directions (both vertical and horizontal.)

Notice that in this question, the signs of the external force (
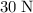`30\; {\rm N}`) and normal force (
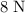`8\; {\rm N}`) are positive, while the sign of weight (
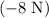`(-8\; {\rm N})`) is negative. This notation suggests that upward and along the direction of the force pushing on the box are positive directions. Forces that act in the opposite direction (e.g., downward, as in weight) would have a negative sign.

List all the forces on this box. Forces in the vertical direction are:

• Weight of the box:
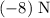  `(-8)\; {\rm N}` (negative since the force points downward,) and
• Normal force from the floor:
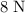  `8\; {\rm N}` (upward.)

Since these two force are of equal magnitude (
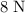`8\; {\rm N}`) and opposite in directions, they balance each other. Thus, the resultant force in the vertical direction would be
`0\; {\rm N}` as expected.

Similarly, forces on the box in the horizontal direction are:

• External force pushing on the box:
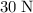  `30\; {\rm N}`, and
• Friction from the floor.

Similar to the vertical direction, the resultant force in the horizontal direction should also be
`0\; {\rm N}`. Thus, friction should have the same magnitude as the
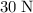`30\; {\rm N}` external force. However, since friction would be opposite to the positive horizontal direction (direction of this force pushing on the box,) the sign of friction on the box would be negative.

Therefore, the friction on the box should be
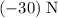`(-30)\; {\rm N}`.