Question

4. Find the value of x for which ABCD must be a parallelogram.

Answer 1

Here is your answer!!

Properties of Parallelogram :

1. Opposite sides are equal.
2. Opposite sides are parallel
3. Adjacent angles add upto 180°.
4. Opposite angles are equal.

Here in the question we are provided with opposite sides 3x- 5 and 2x + 3 .

Therefore, First property of Parallelogram will be used here and both the opposite sides must be equal.

`\sf 3x- 5 = 2x + 3`

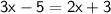
Further solving for value of x

Move all terms containing x to the left, all other terms to the right.

`\sf 3x - 2x = 3 + 5`

`\sf 1x = 8`

`\sf x = 8`

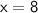
Let's verify our answer!!

Since, 3x- 5 = 2x + 3

We are simply verify our answer by substituting the value of x here.

`\sf 3x- 5 = 2x + 3`

`\sf 3(8) - 5 = 2(8) + 3`

`\sf 24 - 5 = 16 + 3`

`\sf 19 = 19`

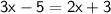
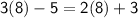
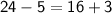
Hence our answer is verified and value of x is 8

Answer - Option 1