Question

In the figure given below, let the lines l1 and l2 be parallel and t is transversal. Find the value of x

Answer 1

In the figure given, the lines
`\sf l_1` and
`\sf l_2` are parallel and t is transversal.

Parallel Lines and Transversal :

If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent.

In the figure we can see that 2x + 20 and 3x - 10 are the corresponding angles

So,

`\sf 2x + 20 = 3x - 10`

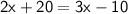
further solving for value of x

`\sf 2x + 20 = 3x - 10`

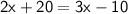
Move all terms containing x to the left, all other terms to the right.

`\sf 2x - 3x = -10 - 20`

`\sf -1x = -30`

`\sf x = (- 30)/(-1 )`

`\sf x = 30`

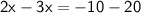
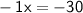
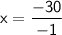
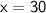
Therefore the value of x is 30

We can also verify our answer.

Since 2x + 20 and 3x - 10 are the corresponding angles .

`\sf 2x + 20 = 3x - 10`

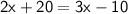
Simply by the putting the value of x here we can verify our answer.

`\sf 2 (30) + 20 = 3(30) - 10`

`\sf 60 + 20 = 90 - 10`

`\sf 80 = 80`

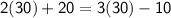
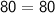
Hence our answer is verified.

Hence the Value of x is 30