Question

Can anyone help me with this question please

Answer 1

Explanation:

all the functions with the "exponent" -1 mean inverse function (and not 1/function).

the inverse function gets a y value as input and delivers the corresponding x value as result.

so,

`g { }^( - 1) (0)`

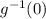
gets 0 as input y value. now, what was the x value in g(x) that delivered 0 ?

4

that x value delivering 0 as y was 4.

so,

`g {}^( - 1) (0) = 4`

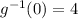
the inverse function for a general, continuous function get get by transforming the original functional equation, so that x is calculated out of y :

h(x) = y = 4x + 13

y - 13 = 4x

x = (y - 13)/4

and now we rename x to y and y to x to make this a "normal" function :

y = (x - 13)/4

so,

`h {}^( - 1) (x) = (x - 13) / 4`

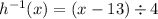
a combined function (f○g)(x) means that we first calculate g(x) and then use that result as input value for f(x). and that result is then the final result.

formally, we simply use the functional expression of g(x) and put it into every occurrence of x in f(x).

so, we have here

4x + 13

that we use in the inverse function

((4x + 13) - 13)/4 = (4x + 13 - 13)/4 = 4x/4 = x

the combination of a function with its inverse function always delivers the input value x unchanged.

so,

(inverse function ○ function) (-3) = -3

Answer 2

`\text{g}^(-1)(0) =\boxed{4}`

`h^(-1)(x)=\boxed{(x-13)/(4)}`

`\left(h^(-1) \circ h\right)(-3)=\boxed{-3}`

Explanation:

The inverse of a one-to-one function is obtained by reflecting the original function across the line y = x, which swaps the input and output values of the function. Therefore, (x, y) → (y, x).

Given the one-to-one function g is defined as:

`\text{g}=\left\{(-7,-3),(0,2),(1,3),(4,0),(8,7)\right\}`

Then, the inverse of g is defined as:

`\text{g}^(-1)=\left\{((-3,-7),(2,0),(3,1),(0,4),(7,8)\right\}`

Therefore, g⁻¹(0) = 4.

`\hrulefill`

To find the inverse of function h(x) = 4x + 13, begin by replacing h(x) with y:

`y=4x+13`

Swap x and y:

`x=4y+13`

Rearrange to isolate y:

`\begin{aligned}x&=4y+13\\\\x-13&=4y+13-13\\\\x-13&=4y\\\\4y&=x-13\\\\(4y)/(4)&=(x-13)/(4)\\\\y&=(x-13)/(4)\end{aligned}`

Replace y with h⁻¹(x):

`\boxed{h^(-1)(x)=(x-13)/(4)}`

`\hrulefill`

As h and h⁻¹ are true inverse functions of each other, the composite function (h o h⁻¹)(x) will always yield x. Therefore, (h o h⁻¹)(-3) = -3.

To prove this algebraically, calculate the original function of h at the input value x = -3, and then evaluate the inverse of function h at the result.

`\begin{aligned}\left(h^(-1)\circ h \right)(-3)&=h^(-1)\left[h(-3)\right]\\\\&=h^(-1)\left[4(-3)+13\right]\\\\&=h^(-1)\left[1\right]\\\\&=(1-13)/(4)\\\\&=(-12)/(4)\\\\&=-3\end{aligned}`

Hence proving that (h⁻¹ o h)(-3) = -3.