Question

Inverse functions Linear Discrete please help

Answer 1

`\text{g}^(-1)(1) =\boxed{2}`

`h^(-1)(x)=\boxed{-5x-3}`

`\left(h \circ h^(-1)\right)(-1)=\boxed{-1}`

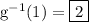
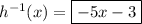
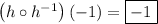
Explanation:

The inverse of a one-to-one function is obtained by reflecting the original function across the line y = x, which swaps the input and output values of the function. Therefore, (x, y) → (y, x).

Given the one-to-one function g is defined as:

`\text{g}=\left\{(-8,5), (-4,-8), (1,-4), (2,1)\right\}`

Then, the inverse of g is defined as:

`\text{g}^(-1)=\left\{(5,-8), (-8,-4), (-4,1), (1,2)\right\}`

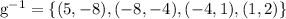
Therefore, g⁻¹(1) = 2.

`\hrulefill`

To find the inverse of function h(x), begin by replacing h(x) with y:

`y=(-x-3)/(5)`

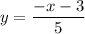
Swap x and y:

`x=(-y-3)/(5)`

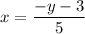
Rearrange to isolate y:

`5 \cdot x=5 \cdot (-y-3)/(5)`

`5x=-y-3`

`5x+y=-y-3+y`

`5x+y=-3`

`5x+y-5x=-3-5x`

`y=-5x-3`

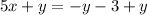
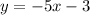
Replace y with h⁻¹(x):

`\boxed{h^(-1)(x)=-5x-3}`

`\hrulefill`

As h and h⁻¹ are true inverse functions of each other, the composite function (h o h⁻¹)(x) will always yield x. Therefore, (h o h⁻¹)(-1) = -1.

To prove this algebraically, calculate the inverse function of h at the input value x = -1, and then evaluate the original function h at the result.

`\begin{aligned}\left(h \circ h^(-1)\right)(-1)&=h\left[h^(-1)(-1)\right]\\\\&=h\left[-5(-1)-3\right]\\\\&=h\left[5-3\right]\\\\&=h\left[2\right]\\\\&=(-(2)-3)/(5)\\\\&=(-5)/(5)\\\\&=-1\end{aligned}`

Hence proving that (h o h⁻¹)(-1) = -1.