Question

prove, using albegra, that the difference between the squares of consecutive even numbers is always a multiple of 4

Answer 1

Let's start by representing the two consecutive even numbers as x and x+2. Then, the difference between their squares can be expressed as:

(x+2)^2 - x^2

Expanding the squares and simplifying, we get:

(x^2 + 4x + 4) - x^2

Which simplifies further to:

4x + 4

Factoring out 4, we get:

4(x + 1)

This shows that the difference between the squares of consecutive even numbers is always a multiple of 4. Therefore, we have proven algebraically that the statement is true for all even numbers.

Answer 2

See below for proof.

Explanation:

An even number is an integer (a whole number that can be either positive, negative, or zero) that is divisible by 2 without leaving a remainder. Therefore:

• 2n is an even number.

Consecutive even numbers are a sequence of even numbers that increase by 2 with each successive number. Therefore:

• 2n + 2 is the consecutive even number of 2n.

The difference between the squares of consecutive even numbers can be written algebraically as:

`(2n + 2)^2 - (2n)^2`

Use algebraic manipulation to rewrite the expression:

`\begin{aligned}(2n + 2)^2 - (2n)^2&=(2n+2)(2n+2)-(2n)(2n)\\&=4n^2+4n+4n+4-4n^2\\&=4n^2-4n^2+4n+4n+4\\&=8n+4\\&=4(2n+1)\end{aligned}`

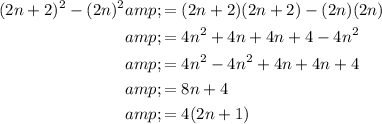
As the common factor of 4 can be factored out of the expression, this proves that the difference between the squares of consecutive even numbers is always a multiple of 4.