Question

Answer the following question

Answer 1

Statement (B) and (C) are true.

Explanation:

We are given a function that represents the spread of a rumor among a group of people in an enclosed space. The function is given as follows:

`N(t)=(300)/(1+299e^(-0.36t))`

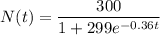
We want to determine which of these following statements are true.

(A) The rumor spreads at a constant rate of 0.36 people per minute.

(B) There are 300 people in the enclosed space.

(C) Initially, only one person had heard the rumor.

(D) It will take 30 minutes for 100 people to hear the rumor.
`\hrulefill`

Determining if (A) is true or not:

To determine if the rumor spreads at a constant rate, we need to find the derivative of the function N(t) with respect to time, t, and check if it is a constant.

`N(t)=(300)/(1+299e^(-0.36t))`

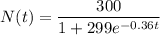
To find the derivative, we can apply the quotient rule:

`\boxed{\left\begin{array}{ccc}\text{\underline{The Quotient Rule:}}\\\\(d)/(dx)\Big[(f(x))/(g(x)) \Big]=(g(x)f'(x)-f(x)g'(x))/((g(x))^2) \end{array}\right}`

`\Longrightarrow N'(t)=((1+299e^(-0.36t))(0)-(300)((299\cdot -0.36)e^(-0.36t)))/((1+299e^(-0.36t))^2)`

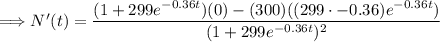
Simplifying further:

`\Longrightarrow N'(t)=((300)(107.64)e^(-0.36t)))/((1+299e^(-0.36t))^2)\\\\\\\Longrightarrow \boxed{ N'(t)=(32292e^(-0.36t)))/((1+299e^(-0.36t))^2)}`

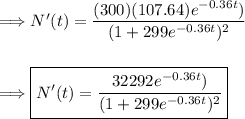
The derivative N'(t) is a function that depends on t. If this function were a constant, it would imply that the rate of spread is constant over time.

To test if N'(t) is a constant, we can examine its behavior by considering different values of t. If the resulting values are the same, then N'(t) is constant.

Let's evaluate N'(t) at two different values of t, let's say t = 0 and t = 1:

At t = 0:

`N'(0)=(32292e^(-0.36(0))))/((1+299e^(-0.36(0)))^2)\\\\\\N'(0)\approx0.36`

At t = 1:

`N'(1)=(32292e^(-0.36(1))))/((1+299e^(-0.36(1)))^2)\\\\\\N'(1) \approx 0.51`

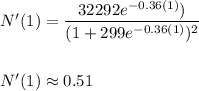
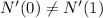`N'(0) \\eq N'(1)`, thus we can conclude that the rate speeds up rather than remain at a constant rate. Statement (A) is false.

Determining if (B) is true or not:

If we take the limit as t approaches infinity, we can determine the behavior of the function and infer the value for statement B.

`\lim_(t \to \infty) N(t)= \lim_(t \to \infty) (300)/(1+299e^(-0.36t))`

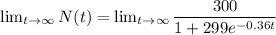
As t approaches infinity, the exponential term e^{-0.36t} approaches 0, making the denominator approach 1.

`\lim_(t \to \infty) N(t)= \lim_(t \to \infty) (300)/(1+0)= \boxed{300}`

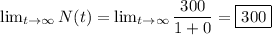
Therefore, according to the given function, as time goes to infinity, the number of people who have heard the rumor approaches 300. This confirms that statement (B) is true: there are 300 people in the enclosed space.

Determining if (C) is true or not:

To find the initial amount of people who heard the rumor, we can plug in t = 0 into the function and evaluate N(0).

`N(0)=(300)/(1+299e^(-0.36(0)))`

Since e^0 is equal to 1, the exponential term becomes 1, and the denominator simplifies to (1 + 299).

`N(t)=(300)/(1+299)=(300)/(300) =\boxed{1}`

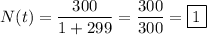
Therefore, according to the given function, initially, only one person had heard the rumor. This confirms that statement (C) is true.

Determining if (D) is true or not:

To determine the validity of statement (D), we can substitute t = 30 into the function and check if N(t) equals 100.

`N(30)=(300)/(1+299e^(-0.36(30)))`

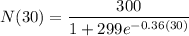
Calculating this expression will give us the number of people who have heard the rumor after 30 minutes. If the result is 100, then the statement is true.

`N(30)\approx298`

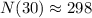
Since N(30) is approximately 298, which is not equal to 100. Therefore statement (D) is false.

`\hrulefill`

Thus, we have concluded only statements (B) and (C) are true.