Question

Answer the following question

Answer 1

Option (C), t≈33 min

Explanation:

Using Newton's law of cooling to answer the given question.

Given:

`T_0=210 \ \textdegree F\\\\T_a=68 \ \textdegree F\\\\T(10)=200 \ \textdegree F`

Find:

`T(??)=180 \ \textdegree F\\\\\\\hrule`

Newton's law of cooling is given as:

`T(t)=T_a+(T_0-T_a)e^(-kt)`

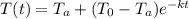
Substitute our know values into the equation.

`\Longrightarrow T(t)=68+(210-68)e^(-kt)\\\\\\\Longrightarrow \boxed{T(t)=68+142e^(-kt)}`

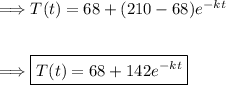
Now using the initial condition to solve for the value of "k."

`T(t)=68+142e^(-kt); \ T(10)=200\\\\\\\Longrightarrow 200=68+142e^(-k(10))\\\\\\\Longrightarrow 132=142e^(-10k)\\\\\\\Longrightarrow (66)/(71) =e^(-10k)\\\\\\\Longrightarrow \ln\Big((66)/(71)\Big) =-10k\\\\\\\Longrightarrow k=(\ln\Big((66)/(71)\Big))/(-10) \\\\\\\therefore k \approx 0.007303`

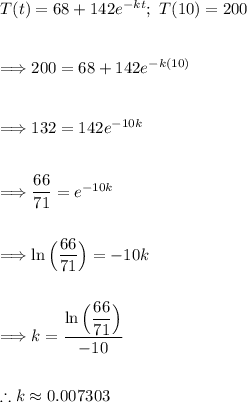
Now we have the following function,

`T(t)=68+142e^(-0.007303t)`

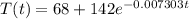
Finding the value of "t" now.

`\Longrightarrow 180=68+142e^(-0.007303t)\\\\\\\Longrightarrow 112=142e^(-0.007303t)\\\\\\\Longrightarrow (56)/(71)=e^(-0.007303t)\\\\\\\Longrightarrow \ln\Big((56)/(71)\Big)=-0.007303t\\\\\\\Longrightarrow t=(\ln\Big((56)/(71)\Big))/(-0.007303) \\\\\\\therefore \boxed{\boxed{t \approx 33 \ min}}`

Thus, option (C) is correct.