Question

PLEASE HELP 100 POINTS

Select the correct answer.
The length, l, of a rectangle is modeled by the equation l = w + 4, where w is the width of the rectangle in centimeters.

Two equations have been determined that represent the area of the rectangle, A, in square centimeters:

The first equation was created using the formula for the area of a rectangle: A = w2 + 4w.
The second equation models the relationship between the rectangle's area and width: A = 4w + 45.
Which statement describes the solution(s) of the system?

A.
There are two solutions, and neither are viable.
B.
There are two solutions, but only one is viable.
C.
There are two solutions, and both are viable.
D.
There is only one solution, and it is viable.

Answer 1

B) There are two solutions, but only one is viable.

Explanation:

Given system of equations:

`\begin{cases}A=w^2+4w\\A=4w+45\end{cases}`

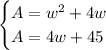
To solve the system of equations, substitute the first equation into the second equation:

`w^2+4w=4w+45`

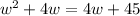
Solve for w using algebraic operations:

`\begin{aligned}w^2+4w&=4w+45\\w^2+4w-4w&=4w+45-4w\\w^2&=45\\√(w^2)&=√(45)\\w&=\pm √(45)\\w &\approx \pm 6.71\; \sf cm\end{aligned}`

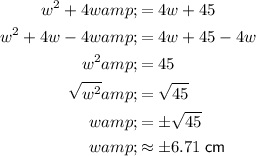
Therefore, there are two solutions to the given system of equations.

However, as length cannot be negative, the only viable solution is w ≈ 6.71 cm.