Question

Find r if 0=pi/6 rad sector 64m^2

Answer 1

Given:

Area of a sector = 64 m²

The central angle is
`\theta=(\pi)/(6)`.

To find:

The radius or the value of r.

Solution:

Area of a sector is:

`A=(1)/(2)r^2\theta`

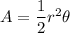
Where, r is the radius of the circle and
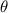`\theta` is the central angle of the sector in radian.

Putting
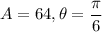`A=64,\theta=(\pi)/(6)`, we get

`64=(1)/(2)r^2* (\pi)/(6)`

`64=(\pi)/(12)r^2`

`64* (12)/(\pi)=r^2`

`(768)/(\pi)=r^2`

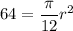
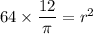
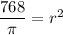
Taking square root on both sides, we get

`\sqrt{(768)/(\pi)}=r`

`16\sqrt{(3)/(\pi)}=r`

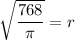
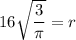
Therefore, the value of r is
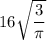`16\sqrt{(3)/(\pi)}` m.