Given:
Area of a sector = 64 m²
The central angle is
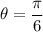 .
.
To find:
The radius or the value of r.
Solution:
Area of a sector is:
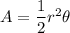
Where, r is the radius of the circle and
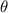 is the central angle of the sector in radian.
is the central angle of the sector in radian.
Putting
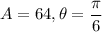 , we get
, we get
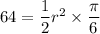
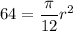
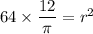
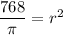
Taking square root on both sides, we get
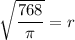
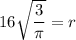
Therefore, the value of r is
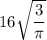 m.
m.