Question

Solve the system of equations using eigenvalues and eigenvectors:  dx/dt=4y  dy/dt=−5x+8y [alt form: dx/dt=4y,dy/dt=−5x+8y ]

Answer 1

The eigenvalues of the coefficient matrix in this system of equations are
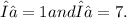`λ₁ = 1 and λ₂ = 7.` corresponding eigenvectors are [2, 1] and [-1, 1], respectively.

To solve the system of equations using eigenvalues and eigenvectors, we first need to rewrite the system in matrix form.

Let's denote the column vector
`[dx/dt, dy/dt]`as v and the matrix [x, y] as M.

The system of equations can then be represented as
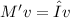`M'v = λv`, where M' is the coefficient matrix.

The coefficient matrix M' is given by:

`M' = [[0, 4], [-5, 8]]`

To find the eigenvalues and eigenvectors, we need to solve the characteristic equation
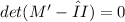`det(M' - λI) = 0`, where I is the identity matrix.

The characteristic equation becomes:

`det([[0, 4], [-5, 8]] - λ[[1, 0], [0, 1]]) = 0`

Simplifying and solving this equation, we find that the eigenvalues are
`λ₁ = 1 and λ₂ = 7.`

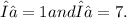
Next, we substitute each eigenvalue back into the equation
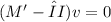`(M' - λI)v = 0` and solve for the corresponding eigenvector.

For λ₁ = 1, we have:

`(M' - λ₁I)v₁ = 0[[0, 4], [-5, 8]]v₁ = 0`

Solving this system of equations, we find the eigenvector
`v₁ = [2, 1].`

For
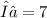`λ₂ = 7`, we have:

`(M' - λ₂I)v₂ = 0[[0, 4], [-5, 8]]v₂ = 0`

Solving this system of equations, we find the eigenvector
`v₂ = [-1, 1].`

Therefore, the eigenvalues of the coefficient matrix are
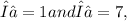`λ₁ = 1 and λ₂ = 7,`and the corresponding eigenvectors are
`v₁ = [2, 1] and v₂ = [-1, 1].`

These eigenvalues and eigenvectors provide a way to solve the given system of equations using diagonalization techniques.