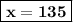Question

An Ontario publishing company mailed 500 brochures to the US and Canada. It

cost $1.10 to mail to the US and $0.80 to mail to Canada. If the total cost was
$440.50, how many were mailed to each country?

Answer 1

135 brochures were mailed to US.

365 brochures were mailed to Canada.

Explanation:

Framing system of equations and solving:

System of linear equations with two variables is a set of two linear equations. We can find the solution of this equations by any one of the following method.

1. Graphical method

2. Substitution method

3. Elimination method.

Here, To find the solution, elimination method is used.

Let the number of brochures mailed to US be 'x'.

Let the number of brochures mailed to Canada be 'y'.

Total brochures = 500

x + y = 500 --------------------------(I)

x = 500 - y ----------------------(II)

Cost of sending 1 mail to US = $1.10

Cost of sending 'x' mail to US = 1.10x

Cost of sending 1 mail to Canada = $0.80

Cost of sending y mail to Canada = 0.80y

Total cost of sending mail = $440.50

1.10x + 0.80y = 440.50

Multiply the entire equation by 10,

11x + 8y = 4405 ---------------------(III)

Substitute x = 500 - y in equation (III),

11*(500 -y) + 8y = 4405

11*500 - 11*y + 8y = 4405

5500 - 11y + 8y = 4405

Subtract 5500 from both sides,

-3y = 4405 - 5500

-3y = -1095

Divide both sides by (-3),

y = -1095 ÷ (-3)

`\boxed{\bf y = 365}`

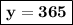
Plug in y = 365 in equation (II)

x = 500 - 365

`\boxed{\bf x = 135}`