Question

Resolve this into partial fraction 5x+2/3x^2+4x-4

Answer 1

`(2)/(3x-2) + (1)/(x+2)`

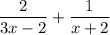
Explanation:

Use partial fraction decomposition to split up the following complex fraction.

`(5x+2)/(3x^2+4x-4)\\\\\\\hrule`

Here's a step-by-step guide on how to perform partial fraction decomposition:

Step 1: Determine the proper form of the fraction

• Make sure the degree of the numerator is less than the degree of the denominator. If it's not, perform long division to reduce the degree of the numerator if necessary.

Step 2: Factor the denominator

• Factorize the denominator of the fraction into linear factors, irreducible quadratic factors, and/or repeated linear factors if possible.
• If the denominator is a polynomial of degree 1 (linear), then it's already factored.
• If the denominator is a polynomial of degree 2 (quadratic), make sure it cannot be factored further.

Step 3: Write the partial fraction decomposition equation

• Write the given fraction as the sum of its partial fraction decomposition. It has the form:

`(A_1)/(factor_1)+ (A_2)/(factor_2) + ... + (A_n)/(factor_n)`

Step 4: Determine the unknown coefficients

• Multiply both sides of the equation obtained in step 3 by the common denominator of the original fraction.
• Equate the numerators on both sides of the equation.
• Solve the resulting system of equations to find the values of the unknown coefficients A₁, A₂, ..., Aₙ.

Step 5: Express the unknown coefficients

• Write the values of the unknown coefficients obtained in step 4.

Step 6: Write the final partial fraction decomposition

• Substitute the values of the unknown coefficients obtained in step 5 back into the partial fraction decomposition equation written in step 3.

• This will give you the final partial fraction decomposition of the given fraction.

Step 7 (Optional): Simplify and evaluate if necessary

• Simplify the resulting expression, combining like terms if possible.

• If you need to evaluate the expression for specific values, substitute the desired values into the simplified expression.

`\hrulefill`

Step 1 -

The degree is determined by the highest power of x that appears in the expression.

`(5x+2)/(3x^2+4x-4)`

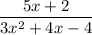
Observing our given expression, we see that the degree of the numerator is 1 and the degree of the denominator is 2. Thus, we can proceed with partial fractions.

Step 2 -

We have,

`3x^2+4x-4`

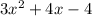
We can factor the denominator using grouping.

`\Longrightarrow 3x^2+4x-4\\\\\\\Longrightarrow 3x^2+(-2+6)x-4\\\\\\\Longrightarrow 3x^2-2x+6x-4\\\\\\\Longrightarrow x(3x-2)+2(3x-2)\\\\\\\Longrightarrow (3x-2)(x+2)`

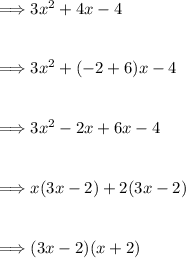
Now we have,

`(5x+2)/(3x^2+4x-4) \Longrightarrow (5x+2)/((3x-2)(x+2))`

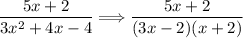
Step 3 -

For step three, instead of writing "A_1, A_2, ..." I will use "A, B, ..."

`(5x+2)/((3x-2)(x+2))=(A)/(3x-2) + (B)/(x+2)`

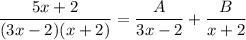
Step 4 and 5 -

`(5x+2)/((3x-2)(x+2))=(A)/(3x-2) + (B)/(x+2) \Big](3x-2)(x+2)\\\\\\\\\Longrightarrow 5x+2=A(x+2)+B(3x-2)\\\\\\\\\Longrightarrow 5x+2=Ax+2A+3Bx-2B\\\\\\\\\Longrightarrow 5x+2=(A+3B)x+(2A-2B)`

Using the method of comparison. We get the following system of equations,

`\left \{ {{5=A+3B} \atop {2=2A-2B}} \right.`

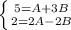
After solving the system we get A=2 and B=1.

Step 6 -

`(5x+2)/((3x-2)(x+2))=\boxed{\boxed{(2)/(3x-2) + (1)/(x+2)}}`

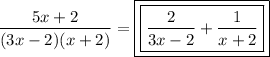
Thus, the problem is solved.