Question

Select the correct answer from each drop-down menu.

The figure shown is made up of a cone and a cylinder. The height of the cone is 5 ft and its diameter is 12 ft. The height of the cylinder is 20 ft.
12 ft.
5 ft
4
20 ft
Find the lateral surface area of the cone and the surface area of the sides and bottom of the cylinder.
The lateral surface area of the cone is about
The total surface area of the figure is about
². The surface area of the sides and the bottom of the cylinder is about
1².
n².

Answer 1

The lateral surface area of the cone is about 147.2 ft².

The surface area of the sides and the bottom of the cylinder is about 867.1 ft².

The total surface area of the figure is about 1014.3 ft².

Explanation:

The formula for the lateral surface area of a cone is:

`\boxed{\begin{minipage}{7 cm}\underline{Lateral Surface Area of a Cone}\\\\$L.S.A.=\pi r √(r^2 + h^2)$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius of the circular base. \\ \phantom{ww}$\bullet$ $h$ is the perpendicular height of the cone.\\\end{minipage}}`

From inspection of the given diagram (attached), we can see that the diameter of the base of the cone is 12 ft.

As the radius of a circle is half its diameter, the radius of the base of the cone is r = 6.

The height of the cone is 5 ft, so h = 5.

Substitute the values of r and h into the formula to calculate the lateral surface area of the cone:

`\begin{aligned}\textsf{Lateral Surface Area of the Cone}&=\pi (6) √(6^2 + 5^2)\\&=6\pi √(36 +25)\\&=6\pi √(61)\\&=6√(61)\pi \\&=147.219738...\\&=147.2\; \sf ft^2\;(nearest\;tenth)\end{aligned}`

The surface area of the cylinder part of the figure is made up of the lateral surface area of the cylinder and the area of one circular base.

Therefore the formula to use to calculate the area of the sides and bottom of the cylinder is:

`\boxed{L.S.A.=2\pi r h+\pi r^2}`

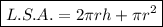
where r is the radius and h is the height of the cylinder.

From inspection of the given diagram, we can see that the radius of the cylinder is r = 6 and the height is h = 20. Substitute these into the formula to find the area of the sides and bottom of the cylinder:

`\begin{aligned}\textsf{S.A. side and bottom of cylinder}&=2 \pi (6)(20)+\pi (6)^2\\&=2 \pi (120)+\pi (36)\\&=240 \pi +36\pi\\&=276 \pi \\&=867.079572...\\&=867.1\; \sf ft^2\;(nearest\;tenth)\end{aligned}`

The total surface area of the figure is the sum of the lateral surface area of the cone and the sides and bottom of the cylinder. Therefore:

`\begin{aligned}\textsf{Total Surface Area}&=147.219738...+867.079572...\\&=1014.29931...\\&=1014.3\; \sf ft^2\;(nearest\;tenth)\end{aligned}`

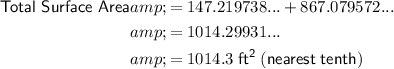
In conclusion:

• The lateral surface area of the cone is about 147.2 ft².
• The surface area of the sides and the bottom of the cylinder is about 867.1 ft².
• The total surface area of the figure is about 1014.3 ft².