Question

URGENT SOLVE TRIGONOMETRY

Answer 1

33.8 m

Explanation:

From the given diagram, we have two right angle triangles, ΔBCD and ΔACD, where:

• CD = 30 m
• m∠CBD = 21°
• m∠CAD = 15°

We want to find the distance between boats A and B, which is line segment AB. To do this we need to subtract the length of line segment BC from the length of line segment AC.

As we have been given the side opposite the angles (CD) and wish to find the sides adjacent the angles, we can use the tangent trigonometric ratio.

`\boxed{\begin{minipage}{7 cm}\underline{Tangent trigonometric ratio} \\\\$\sf \tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle.\\\end{minipage}}`

Triangle ACD

Given values:

• θ = 15°
• O = CD = 30 m
• A = AC

Substitute the values into the tan ratio to create an expression for AC:

`\tan 15^(\circ)=(30)/(AC)`

`AC=(30)/(\tan 15^(\circ))`

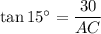
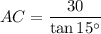
Triangle BCD

Given values:

• θ = 21°
• O = CD = 30 m
• A = BC

Substitute the values into the tan ratio to create an expression for AC:

`\tan 21^(\circ)=(30)/(BC)`

`BC=(30)/(\tan 21^(\circ))`

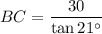
To find the length of line segment AB (the distance between boats A and B), subtract the length of line segment BC from the length of line segment AC.

`\begin{aligned}\overline{AB}&=\overline{AC}-\overline{BC}\\\\&=(30)/(\tan 15^(\circ))-(30)/(\tan 21^(\circ))\\\\&=111.961524...-78.1526719...\\\\&=33.8088522...\\\\&=33.8\; \sf m\;(nearest\;tenth)\end{aligned}`

Therefore, the distance between the two small boats A and B is 33.8 meters (rounded to the nearest tenth).