Question

What is the equation of the line that passes through the point (6,4) and has a slope of 2/3?

Answer 1

The equation is:

`\large\boxed{\quad\tt{y=(2)/(3)x}\quad}`

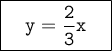
Work/explanation:

Let's write the equation in slope intercept form.

Slope intercept is
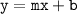`\tt{y=mx+b}`, where m = slope and b = y intercept.

Now let's set up our slope intercept equation, knowing that the slope is 2/3.

`\tt{y=(2)/(3)x+b}`

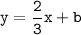
Now, what about b? Well, to find b, I take the point that the line goes through, which is (6,4), and plug that directly into our equation, which, at this stage, is
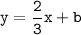`\tt{y=(2)/(3)x+b}`. Note that plugging in the appropriate co-ordinate is important; I plug in 6 for x, and 4 for y.

`\tt{y=(2)/(3)x+b}`

`\tt{4=(2)/(3)(6)+b}`

`\tt{4=4+b}`

`\tt{4-4=b}`

`\tt{0=b}`

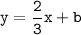
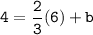
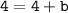
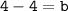
Hence, the equation is
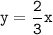`\tt{y=(2)/(3)x}`.

Answer 2

y =
`(2)/(3)` x

Explanation:

the equation of a line in slope- intersect form is

y = mx + c ( m is the slope and c the y- intercept )

here slope m =
`(2)/(3)` , then

y =
`(2)/(3)` x + c ← is the partial equation

to find c substitute (6, 4 ) into the partial equation

4 =
`(2)/(3)` (6) + c = 4 + c ( subtract 4 from both sides )

0 = c

y =
`(2)/(3)` x ← equation of line