Question

a billiard ball traveling at 3.00 m/s collides perfectly elastically with an identical billiard ball initially at rest on the level table. the initially moving billiard ball deflects 30.0° from its original direction. what is the speed of the initially stationary billiard ball after the collision?

Answer 1

`1.5\; {\rm m\cdot s^(-1)}`.

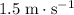Step-by-step explanation:

Since the collision is perfectly elastic, both kinetic energy and momentum should be conserved.

Let
`x` denote the component of the final velocity of the initially-moving billiard ball along the direction of its original motion.

Since this billiard ball is now at an angle of
`30^(\circ)` relative to its initial direction of motion, the component of velocity perpendicular to the direction of motion would be
`x\, \tan(30^(\circ)) = x / √(3)`.

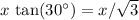Momentum should be conserved in both components. Thus, for the billiard ball that was initially stationary, velocity components after the collision would be:

• 
  `(3.00 - x)` along the initial direction of motion of the incoming billiard ball, and
• 
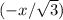  `(-x / √(3))` perpendicular to the direction of motion of the incoming billiard ball.

Before the collision, kinetic energy of the incoming billiard ball would be
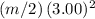`(m/2)\, (3.00)^(2)`, where
`m` is the mass of the billiard ball.

Using the Pythagorean Theorem, the square of the magnitude of each velocity vector would be equal to the sum of the square of individual velocity components.

The kinetic energy of the two billiard balls after the collision would be:

• 
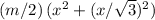  `(m/2)\, (x^(2) + (x / √(3))^(2))` for the incoming billiard ball, and
• 
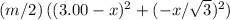  `(m / 2)\, ((3.00 - x)^(2) + (-x / √(3))^(2))` for the billiard ball that was initially stationary.

Since kinetic energy should be conserved:

`\displaystyle (m)/(2)\, (3.00)^(2) = (m)/(2)\, \left(x^(2) + \left((x)/(√(3))\right)^(2)\right) + (m)/(2)\, \left((3.00 - x)^(2) + \left(-(x)/(√(3))\right)^(2)\right)`.

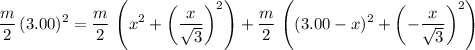Simplify to obtain:

`\displaystyle 3^(2) = x^(2) + (x^(2))/(3) + 3^(2) - 6\, x + x^(2) + (x^(2))/(3)`.

`\displaystyle (8\, x^(2))/(3) - 6\, x = 0`.

`\displaystyle x\, \left((8)/(3)\, x - 6\right) = 0`.

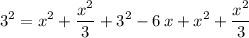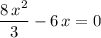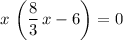Either
`x = 0` or
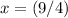`x = (9 / 4)`. However, since the incoming billiard ball is still moving after the collision, velocity of the billiard ball should be non-zero. Hence, only
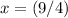`x = (9 / 4)` is a valid solution.

Hence, after the collision, velocity components of the billiard ball that was initial stationary would be:

• 
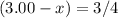  `(3.00 - x) = 3/4` (meters per second) along the initial direction of motion of the incoming billiard ball, and
• 
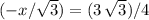  `(-x / √(3)) = (3\, √(3)) / 4` (meters per second) perpendicular to the initial direction of motion of the incoming billiard ball.

The speed (magnitude of velocity) of this billiard ball would be:

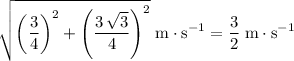`\displaystyle \sqrt{\left((3)/(4)\right)^(2) + \left((3\, √(3))/(4)\right)^(2)}\; {\rm m\cdot s^(-1)} = (3)/(2)\; {\rm m\cdot s^(-1)}`.