Question

Suppose u and v are functions of x that are differentiable at x=0 and that u(0)=-8, u'(0)=-4, v(0)=9, and v'(0)=5. Find the values of the following derivatives at x=0.

Answer 1

(A) -76

(B) 4/81

(C) -1/16

(D) 3

Explanation:

It is given that u and v are functions of x and are differentiable at x=0 and that u(0) = -8, u'(0) = -4, v(0) = 9, and v'(0) = 5. We are asked to find the following derivatives at x=0.

(A) -
`(d)/(dx)[uv]`

(B) -
`(d)/(dx)\Big[(u)/(v) \Big]`

(C) -
`(d)/(dx)\Big[(v)/(u) \Big]`

(D) -
`(d)/(dx) [-5v-7u]`

`\hrulefill`

Part (A) - Using the product rule.

`(d)/(dx)[uv]=uv'+vu'`

Substituting in our values:

`(-8)(5)+(9)(-4)\\\\\\\therefore \boxed{=-76}`

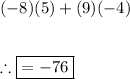
Part (B) - Using the quotient rule.

`(d)/(dx)\Big[(u)/(v) \Big]=(vu'-uv')/(v^2)`

Evaluating at x=0:

`((9)(-4)-(-8)(5))/((9)^2)\\\\\\\therefore \boxed{=(4)/(81) }`

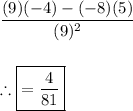
Part (C) - Using the quotient rule.

`(d)/(dx)\Big[(v)/(u) \Big]=(uv'-vu')/(u^2)`

Evaluating at x=0:

`((-8)(5)-(9)(-4))/((-8)^2)\\\\\\\therefore \boxed{=(-1)/(16) }`

Part (D) - Deriving the function.

`(d)/(dx) [-5v-7u]=-5v'-7u'`

Substituting in our values:

`-5(5)-7(-4)\\\\\\\therefore \boxed{=3}`

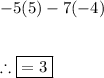
Thus, all parts have been solved.