Answer:
The y-intercept is (0, -3).
The axis of symmetry is x=3/4.
The vertex is (3/4, -21/4).
Explanation:
We are given the following quadratic function.
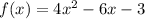
And we are asked to determine the following:
- y-intercept(s)
- Axis of symmetry
- Vertex

To find the y-intercept, axis of symmetry, and vertex of a quadratic function, you can follow these steps:
(1) - Identify the quadratic function: Determine the quadratic function for which you want to find the y-intercept, axis of symmetry, and vertex. It is usually given as an equation or described in a problem.
(2) - Y-intercept: To find the y-intercept, substitute x = 0 into the quadratic function and evaluate the expression. The resulting value represents the y-coordinate of the point where the graph intersects the y-axis.
(3) - Axis of symmetry: The axis of symmetry is a vertical line that passes through the vertex of the quadratic function. To find the axis of symmetry, you can use one of the following methods:
- If the quadratic function is in vertex form, f(x) = a(x - h)² + k, then the axis of symmetry is given by the equation x = h, where (h, k) represents the vertex of the parabola.
- If the quadratic function is in standard form, f(x) = ax² + bx + c, you can use the formula x = -b / (2a) to find the x-coordinate of the vertex.
(4) - Vertex: The vertex of a quadratic function represents the highest or lowest point on the graph (the maximum or minimum point). To find the vertex, you can use one of the following methods:
- If the quadratic function is in vertex form, the vertex is directly given as (h, k).
- If the quadratic function is in standard form, you can substitute the x-coordinate obtained from the axis of symmetry into the function to find the corresponding y-coordinate. The vertex is then represented by the point (x, y).

Step (1) -
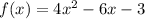
Step (2) -
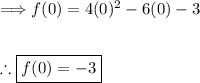
Thus, the y-intercept is (0, -3).
Step (3) -
The given function is in standard form. Thus, we can use the following formula:
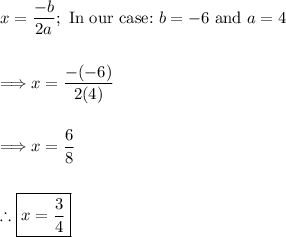
Thus, the axis of symmetry is found.
Step (4) -
Recall that we were given a function in standard form and in step 3 we found that x=3/4.
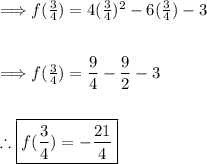
Thus, the vertex is (3/4, -21/4).